ADC's modelleren met behulp van intermodulatiepolynoom en effectief aantal bits

In dit artikel bespreken we een andere methode voor het modelleren van ADC's in systeemsimulaties, dit keer door het effectieve aantal bits te gebruiken en ook onze ADC aan te passen door een 5e-orde polynoom te introduceren bij de ideale kwantiseeringang.

Tot dusverre hebben we in deze serie de voordelen besproken van verschillende manieren om dataconverters in systeemsimulaties te modelleren, met name door een modelleringsmethode te gebruiken die het effectieve aantal bits of ENOB gebruikt.

Nu gaan we deze discussie voortzetten door een nieuw element toe te voegen:ons ADC-model rechtstreeks aanpassen met een 5e-orde polynoom toegevoegd aan de ideale quantizer-invoer.

Beschrijving van ons nieuwe ADC-model

Het model dat in ons vorige artikel werd gepresenteerd, resulteerde niet in duidelijke onechte frequenties (sporen). Omdat sporen een belangrijk kenmerk zijn van ADC-prestaties, was een beter model vereist.

Dit wordt getoond in figuur 1.

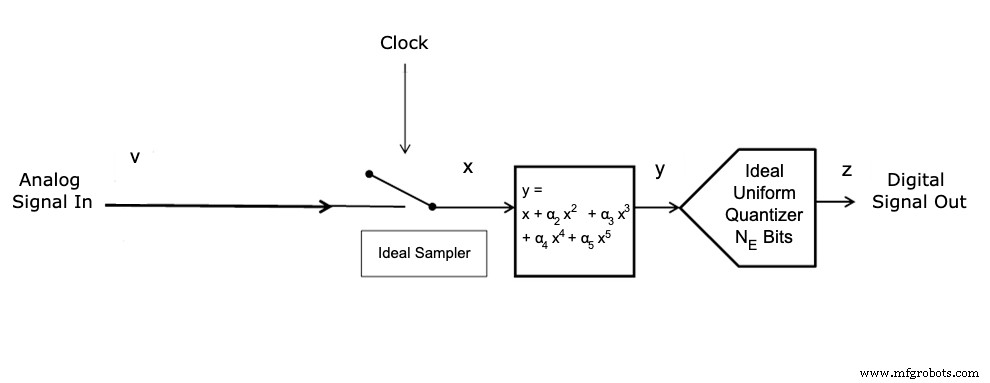
Figuur 1.

Dit voegt een 5e-orde polynoom toe aan de ideale quantizer-invoer.

Er moet een tweekleurige invoer worden gebruikt om de parameters te bepalen α_i (f_c ) en N_E (f_c ); waar f_c is de middenfrequentie tussen de tonen, zoals weergegeven in figuur 2 (die je herkent als figuur 4 uit ons eerste artikel).

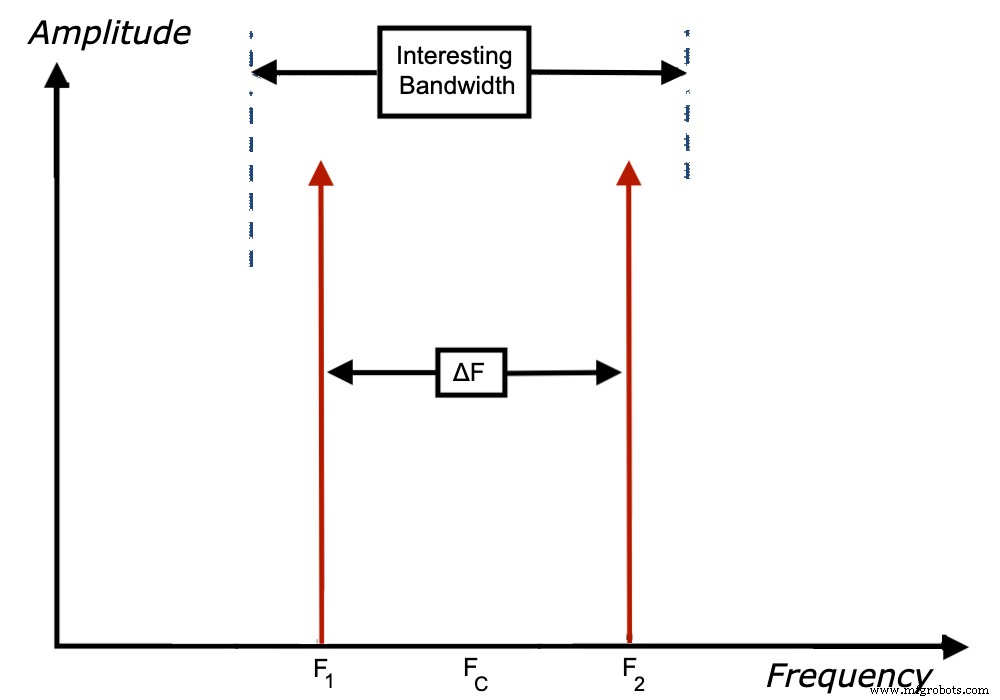
Figuur 2.

Als een van deze parameters ook een functie is van Δf, de scheiding tussen de tonen, is er waarschijnlijk een niet-lineariteit met het geheugen in de ADC en zou dit model niet van toepassing zijn.

Als voorbeeld werd dezelfde tweekleurige invoer als weergegeven in afbeelding 3 (besproken als afbeelding 3 uit ons vorige artikel) gebruikt, met N_E =8 bits, α₃ =0,04, en alle andere α_i =0. Dezelfde Nyquist-bandbreedte (730,9 MHz) en "interessante bandbreedte" (233,7 MHz) als in ons vorige artikel bestaan.

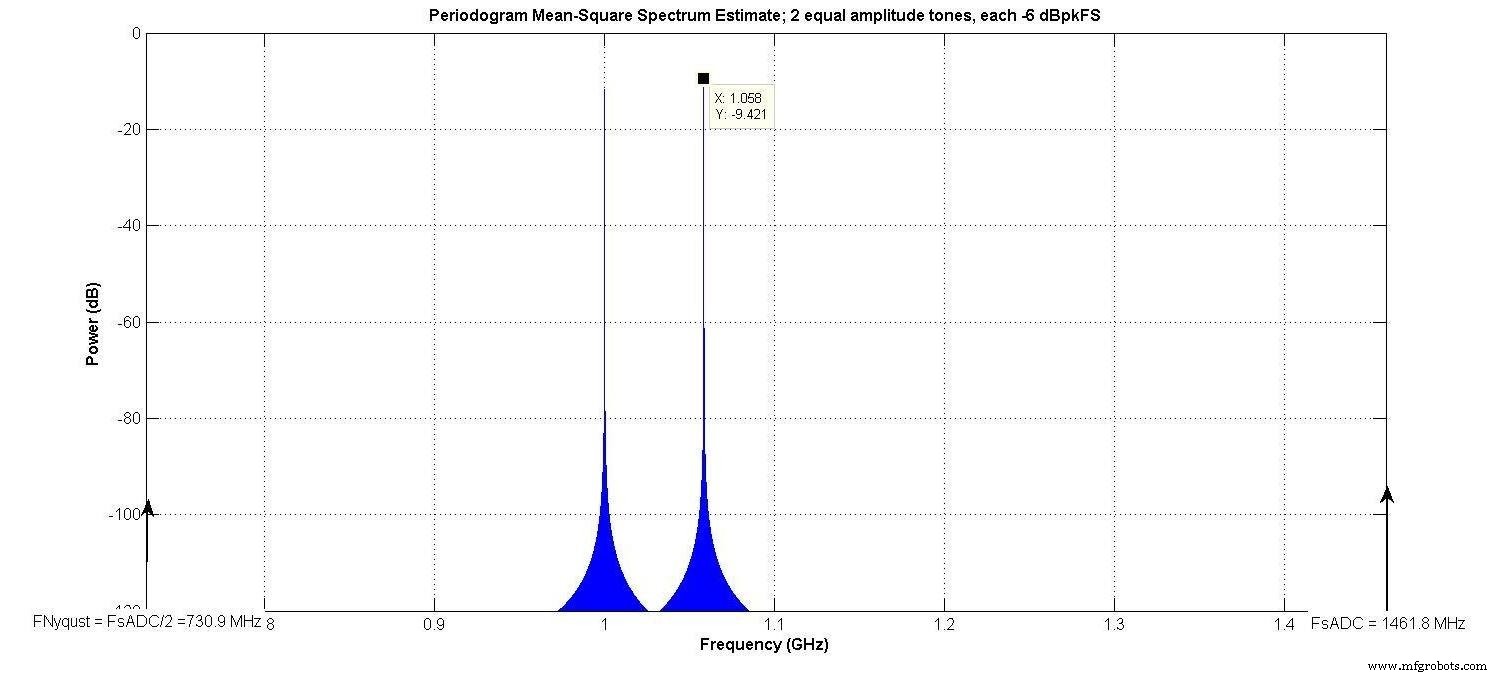
Figuur 3.

Afbeelding 4 toont de uitvoer met eentonige invoer en Afbeelding 5 toont de uitvoer met tweetonige invoer.

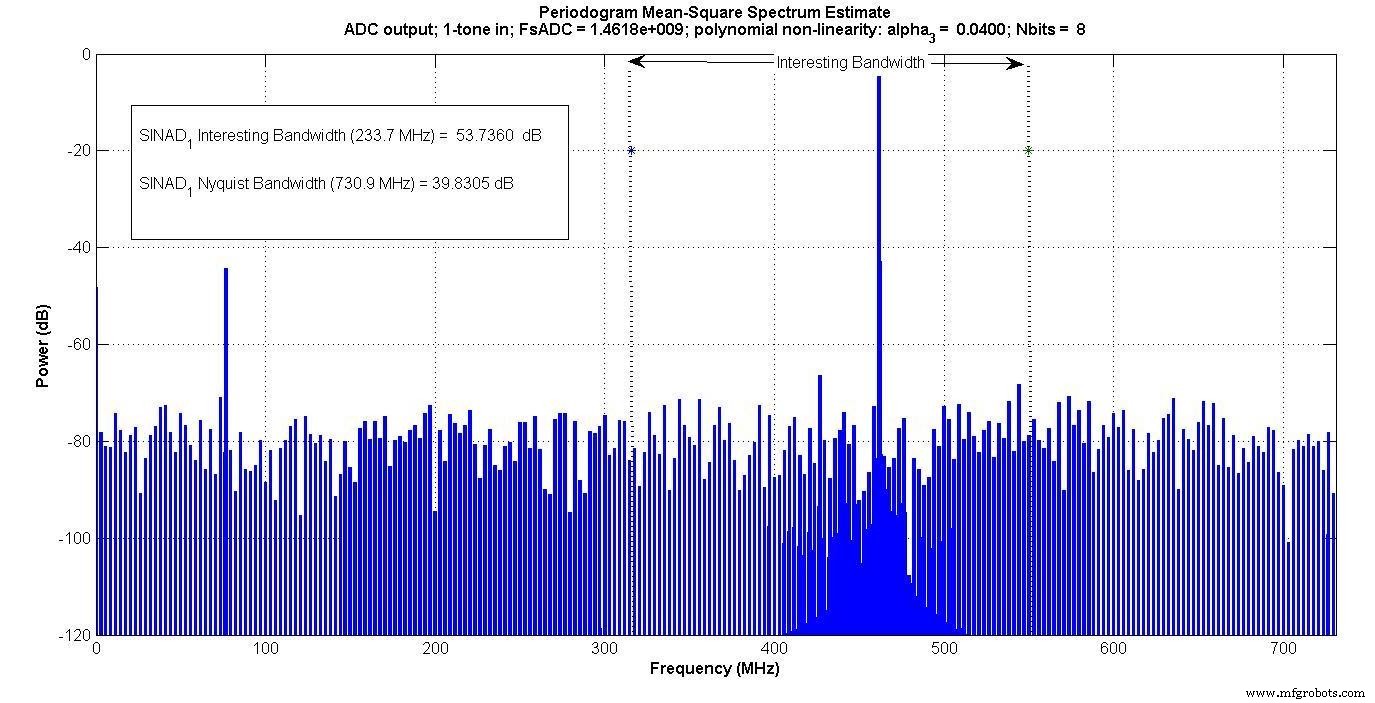
Figuur 4.

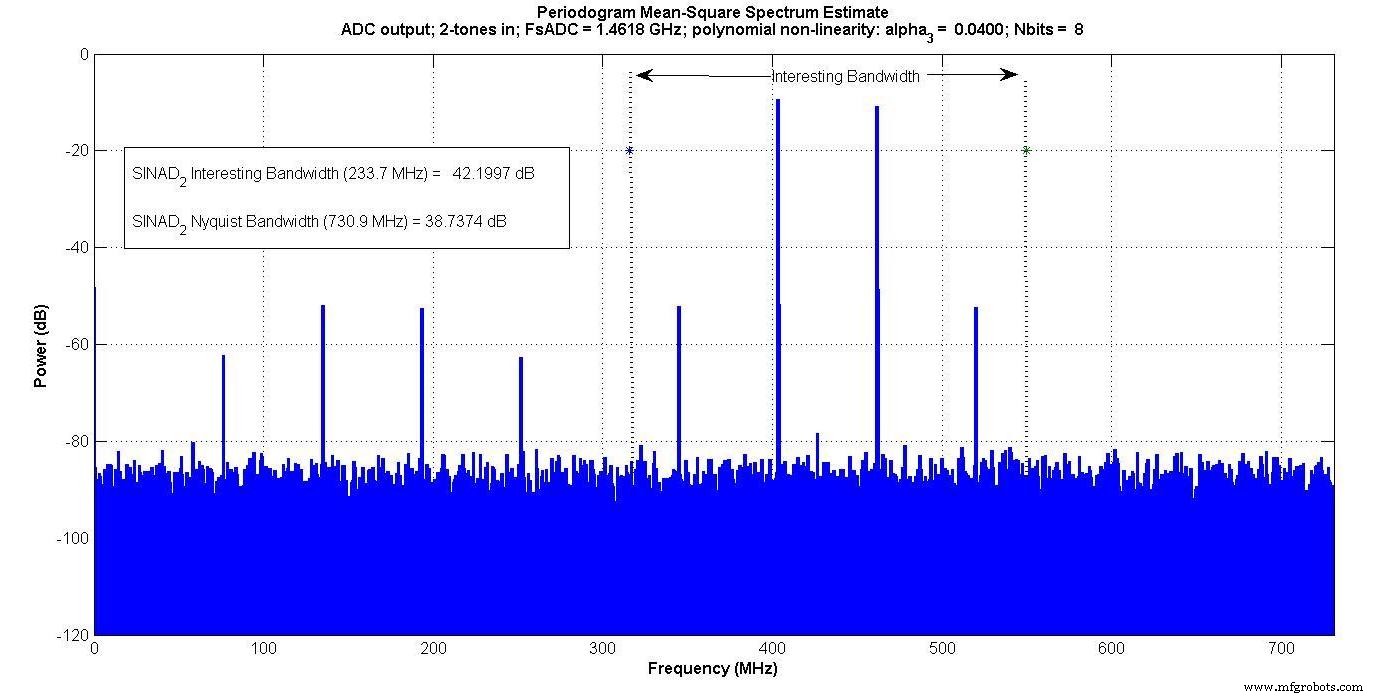
Figuur 5.

Intermodulatieproducten verschijnen binnen de "interessante bandbreedte" voor de tweekleurige ingang, maar niet voor de eenkleurige ingang.

Als iemand alleen binnen deze "interessante bandbreedte" zou meten, bijvoorbeeld als er een digitaal banddoorlaatfilter was dat alleen die band passeerde, zou de eentonige test het intermodulatie-effect niet vastleggen, maar de tweetonige test wel.

Figuur 6 zet de verschillende SINAD's uit voor 5 tot 12 invoerbits. Het is duidelijk dat de eentonige ingang, gemeten in de "interessante bandbreedte", het intermodulatie-effect niet langer dan 7 bits vastlegt.

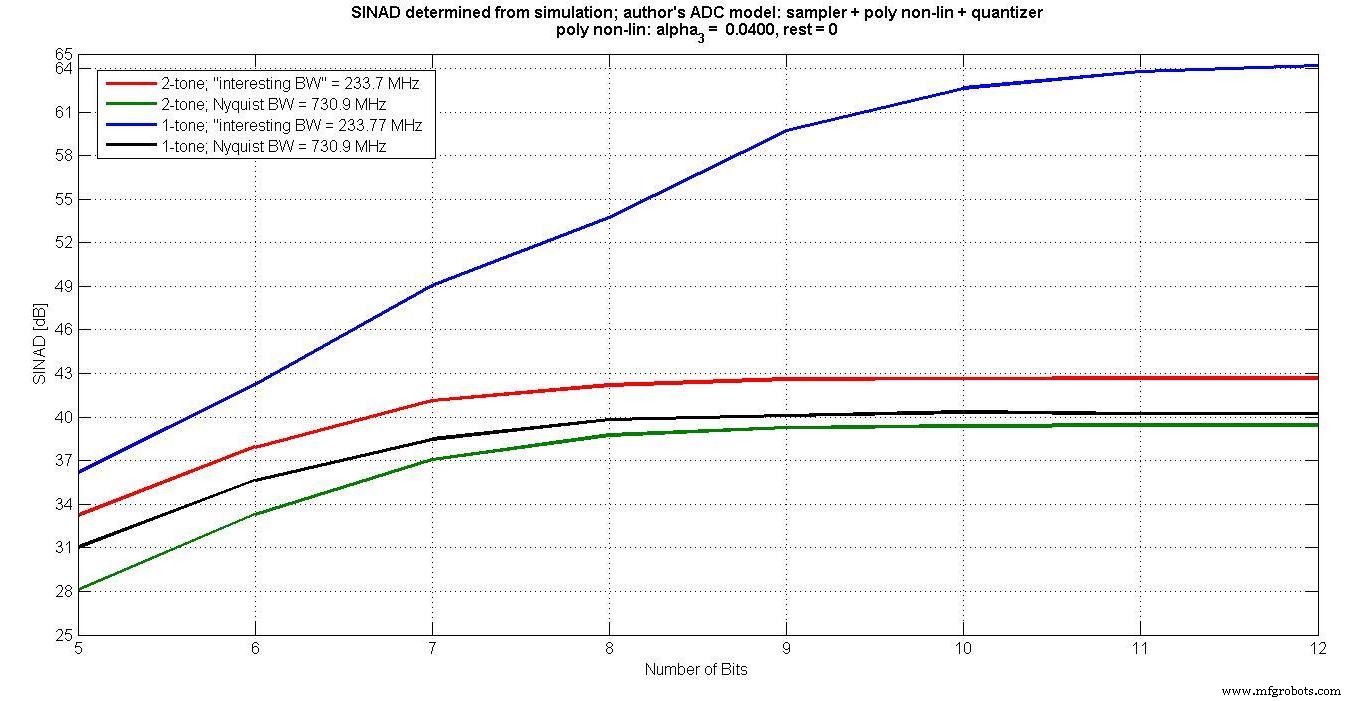
Figuur 6.

Ook voor meer dan 7 bits, aangezien de kwantiseringsruis afneemt naarmate het aantal bits toeneemt, maar de intermodulatievervorming hetzelfde blijft, verbetert de SINAD niet met meer bits.

Vergelijking met het model van de fabrikant

Beste lezer:U vraagt ​​zich nu misschien af; "Dus? Dit zijn slechts enkele modellen en hun reacties op enkele signalen. Wat is het doel?”

Het doel zou moeten zijn dat tweekleurige metingen kunnen worden gedaan op een ADC en dat de parameterwaarden die in figuur 1 worden getoond, worden gekozen om zo goed mogelijk bij de gemeten ADC-uitvoer te passen. Dit kan vaak handmatig worden gedaan totdat een goede pasvorm is verkregen. Vervolgens kan het vereenvoudigde model worden gebruikt in simulaties met een lange bitfoutfrequentie (BER).

De metingen kunnen worden gedaan op een echt apparaat, op een goed model voor het apparaat, of worden verkregen uit de gegevensbladen van de fabrikant.

Om een ​​goed model te zijn, moet het het eigenlijke apparaat goed benaderen; zoals een compleet SPICE-model. Zo'n ingewikkeld model zou te lang duren om in een BER-simulatie te draaien.

Wat voor uw auteur beschikbaar was van een fabrikant, was wat zij een "gedragsmodel" noemden, waarvan zij beweerden dat het alle belangrijke parameters van een bepaald ADC-model vastlegde. Het model van de fabrikant hield ook rekening met zowel interne als externe klokjitter. Dit werd gebruikt om de methode te evalueren.

Tweekleurige invoer

Figuur 7 toont de simulatieopstelling. De tweekleurige invoer is gegenereerd en vervolgens ingevoerd in zowel het model van uw auteur als dat van de fabrikant. Beide werden weergegeven met spectrale analyse.

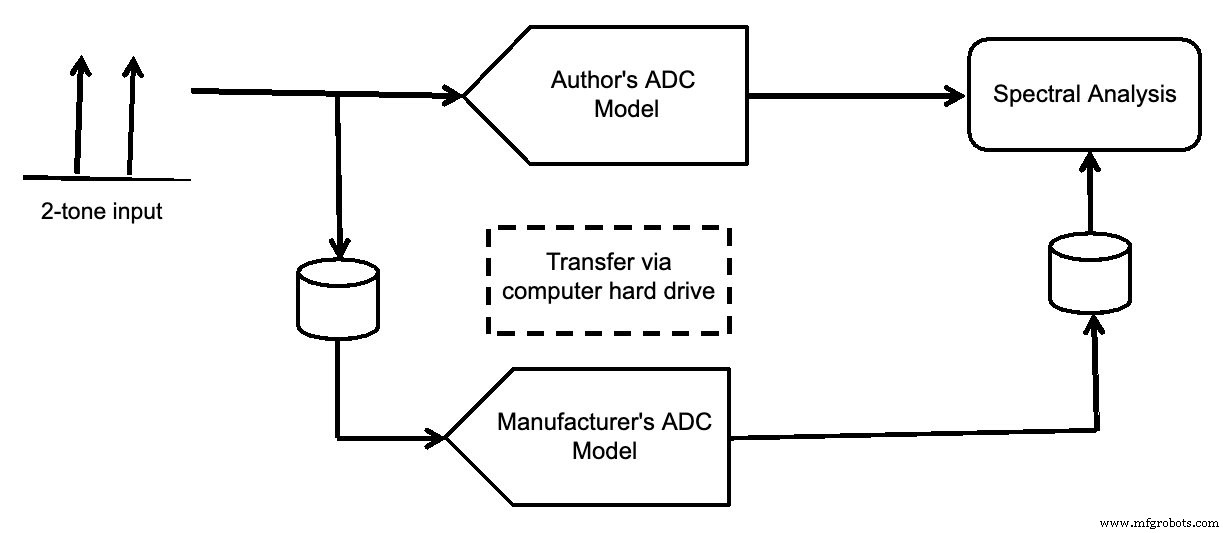
Figuur 7.

Figuur 8 toont de gebruikte invoer. De twee tonen liggen tussen de 300 en 350 MHz. De ADC-bemonsteringsfrequentie is ongeveer 250 MHz, dus deze tonen bevinden zich in de 3e Nyquist-zone.

Aangezien elk -6,02 dBpeakFS is, zal de spanning twee keer zo hoog zijn als ze in fase worden toegevoegd, wat resulteert in 0 dBpeakFS.

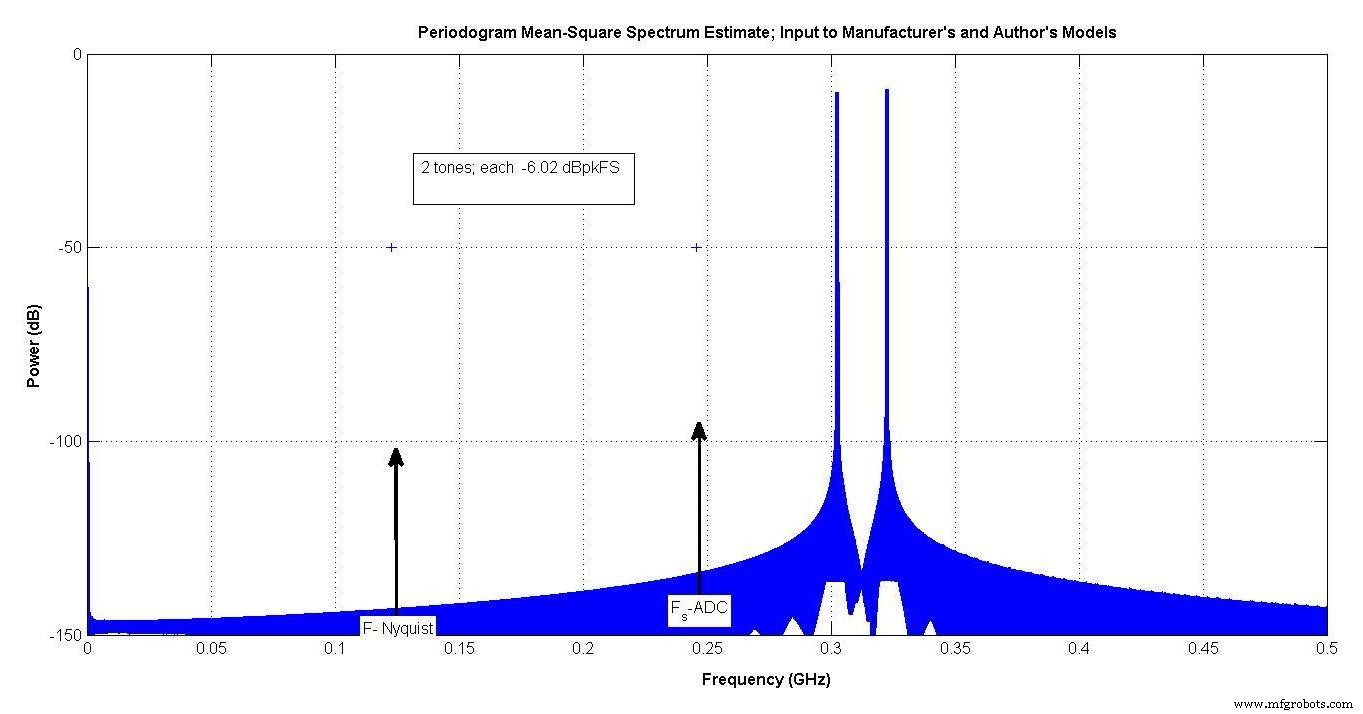
Figuur 8.

Afbeelding 9 toont de output van het model van de fabrikant, dat een SINAD van 63,74 dB had in de "interessante bandbreedte" van ongeveer 27 tot 107 MHz.

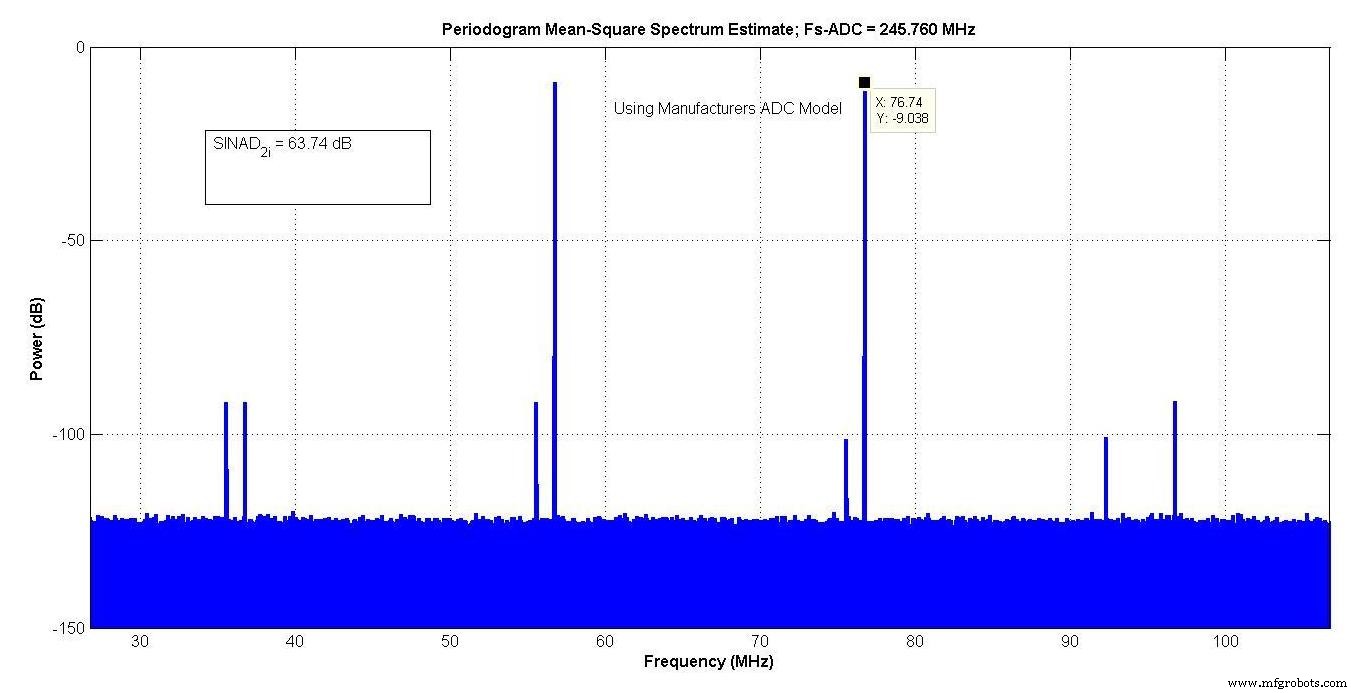
Figuur 9.

Afbeelding 10 toont het resultaat na het aanpassen van de modelparameters van uw auteur voor een overeenkomst.

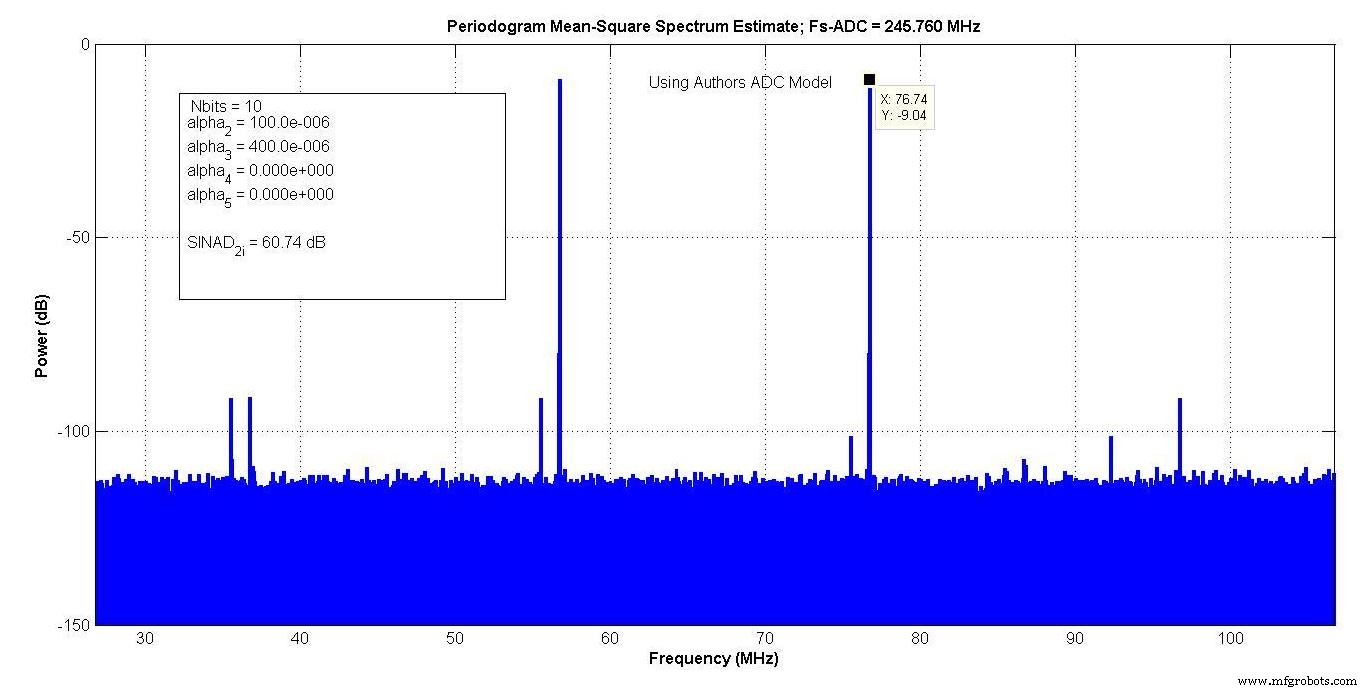
Figuur 10.

De polynomiale coëfficiënten gaven voldoende vrijheidsgraden zodat een bijna exacte match met de sporen kon worden gemaakt. N_E van 11 bits gaf een ruisvloer die 3 dB onder het model van de fabrikant lag, en N_E van 10 bits gaf het 3 dB boven het model van de fabrikant.

Uw auteur heeft besloten de pessimistische waarde van 10 bits te gebruiken, wat een SINAD van 60,74 dB opleverde. Een verbeterd model zou het mogelijk maken om tot 6 dB additieve witte Gauss-ruis toe te voegen, dus de hogere waarde van N_E kan worden gekozen en de extra ruis kan worden toegevoegd om overeen te komen met de ruisvloeren.

OFDM-golfvorminvoer

De twee modellen kunnen nu worden vergeleken met een communicatiegolfvorm als invoer.

Een in de handel verkrijgbaar softwarepakket wordt geleverd met een LTE-model; die een OFDM-signaal genereert. Het model bevat een modulator, een frequentieselectief Rayleigh-fadingkanaal, additieve witte Gauss-ruis en een demodulator.

Het is mogelijk om de ADC-modellen voor de demodulator in te voegen en het spectrum van de ADC-uitgang en de foutvectorgrootte van het OFDM-signaal te evalueren, zoals weergegeven in afbeelding 11.

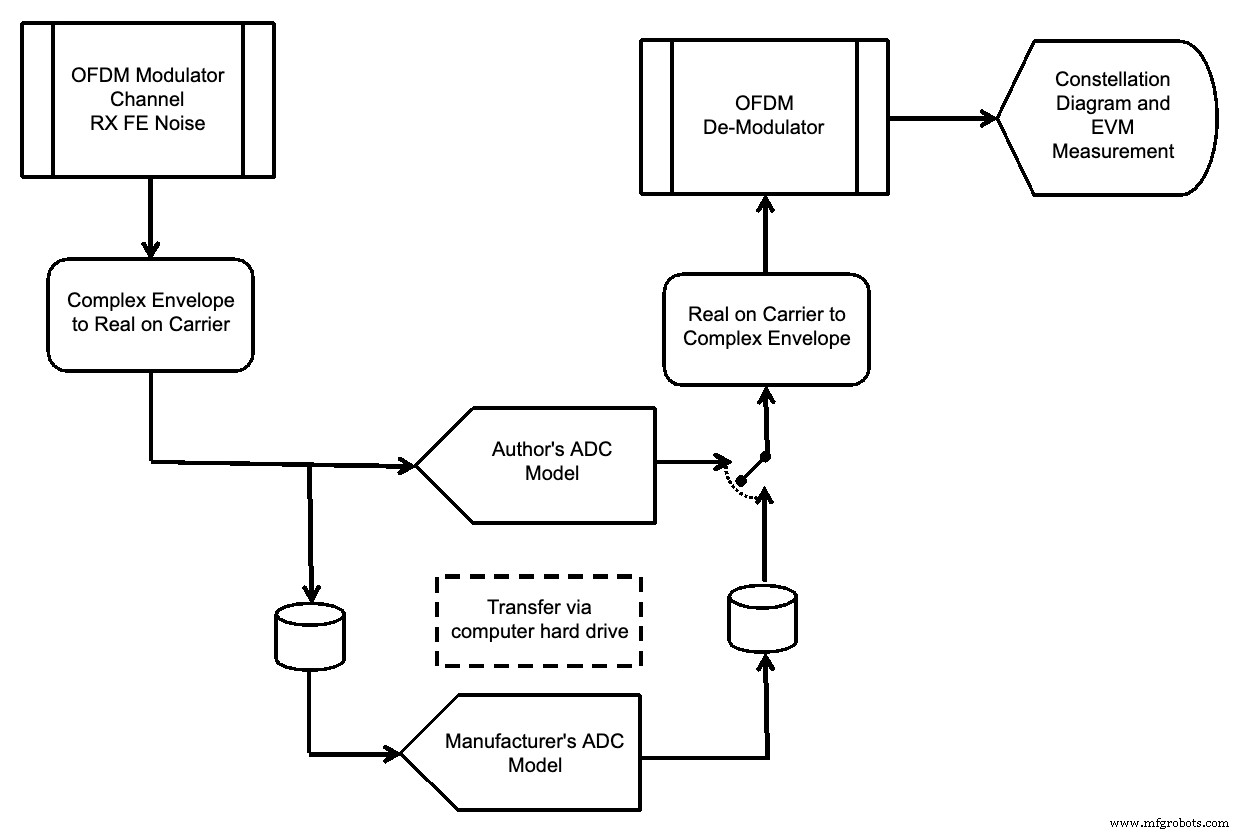
Figuur 11.

Een OFDM-signaal met 64-QAM-hulpdraaggolven werd gebruikt. De parameters van het ADC-model van uw auteur zijn dezelfde als die voor Afbeelding 10.

Het commercieel verkrijgbare softwarepakket gebruikt complexe envelopnotatie [3] om zijn signalen te vormen. Hierdoor kan alleen de modulatie-informatie van monster tot monster worden gevolgd door complexe getallen, en wordt de draaggolffrequentie gewoon als een bekende constante gehouden. Het aantal samples dat nodig is om de golfvorm te beschrijven is dus sterk verminderd.

De ingangen naar de ADC-modellen moeten echter een echt signaal zijn op een expliciete draaggolf, om rekening te houden met het verschil in ADC-prestaties als een functie van de ingangsfrequentie. Dus de transformaties "Complexe envelop naar echt op drager" en "Real op drager naar complexe envelop" [3] moesten worden uitgevoerd.

Afbeelding 12 toont de OFDM-signaalinvoer naar beide ADC-modellen. Het is gecentreerd op dezelfde frequentie als de twee tonen getoond in figuur 8.

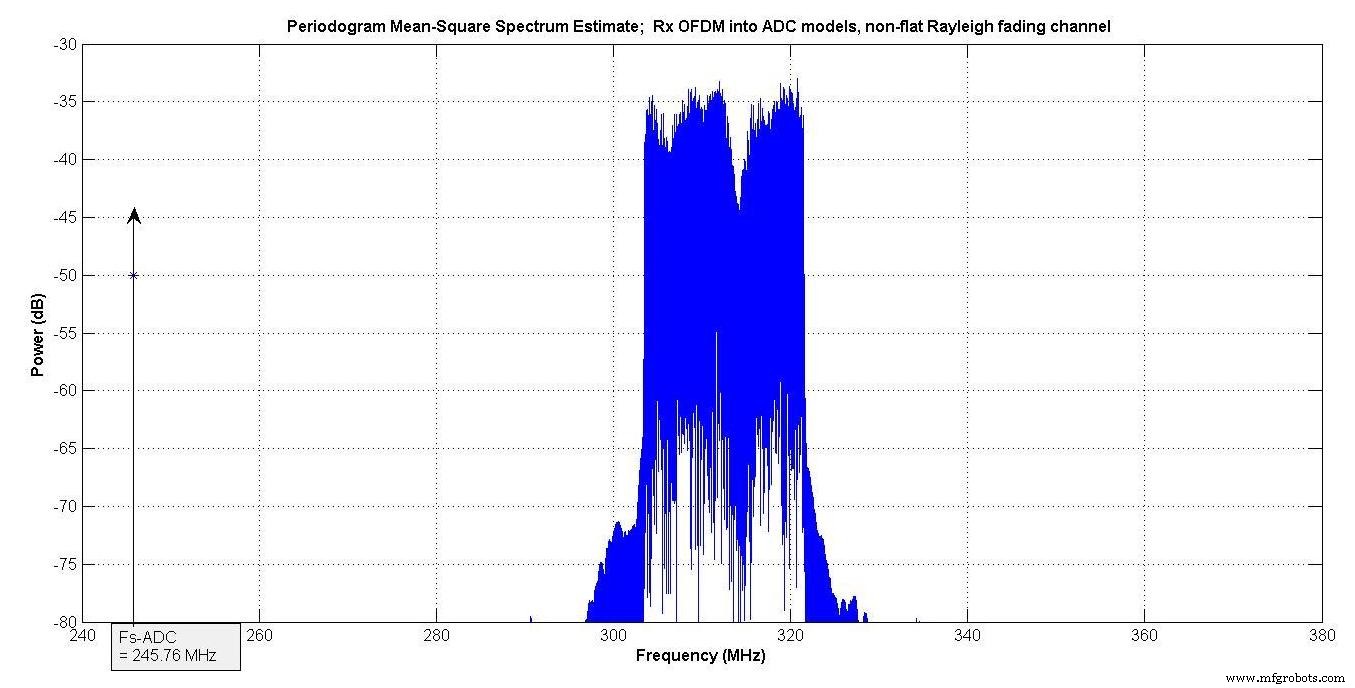
Figuur 12.

Het dBrmsFS-niveau in beide ADC-modellen was -7 dBrmsFS.

Afbeelding 13 toont het spectrum van het model van de fabrikant en Afbeelding 14 dat van het model van uw auteur. Beide vertonen spectrale hergroei vanwege de niet-lineariteit van de ADC's. De spectra zijn heel dichtbij.

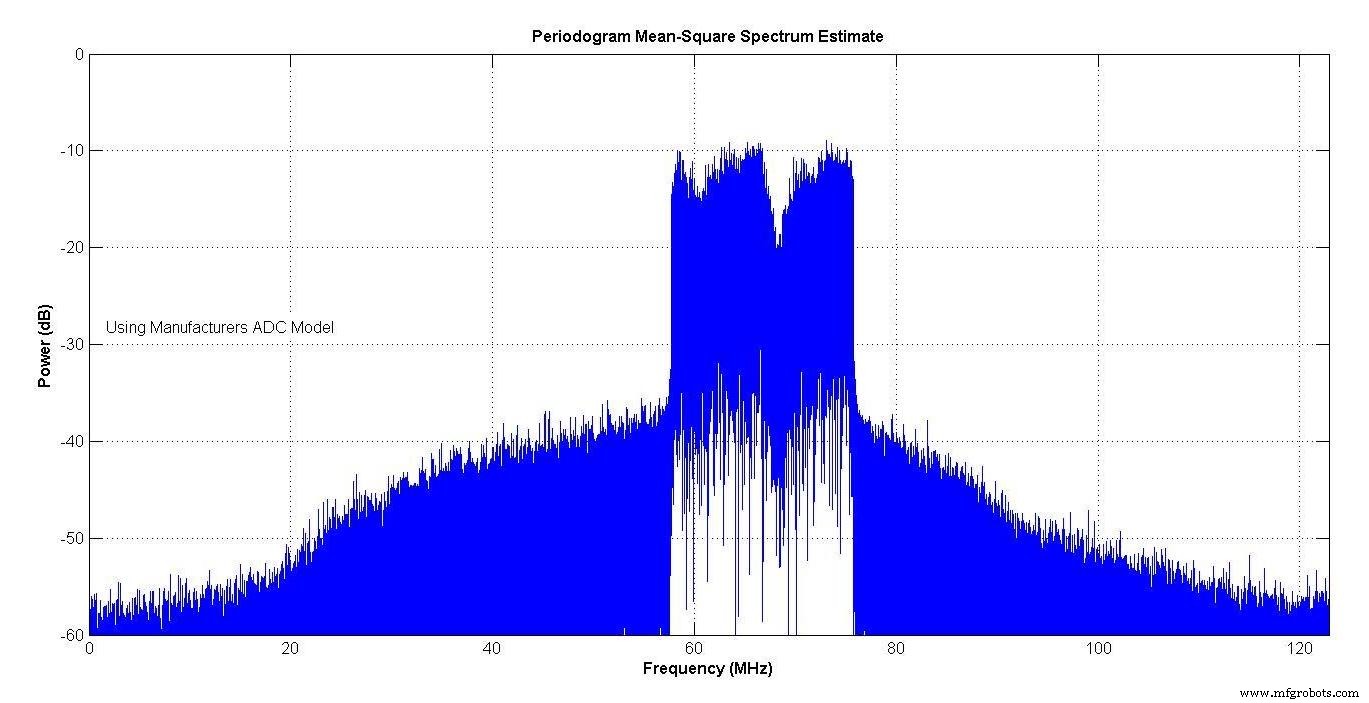
Figuur 13.

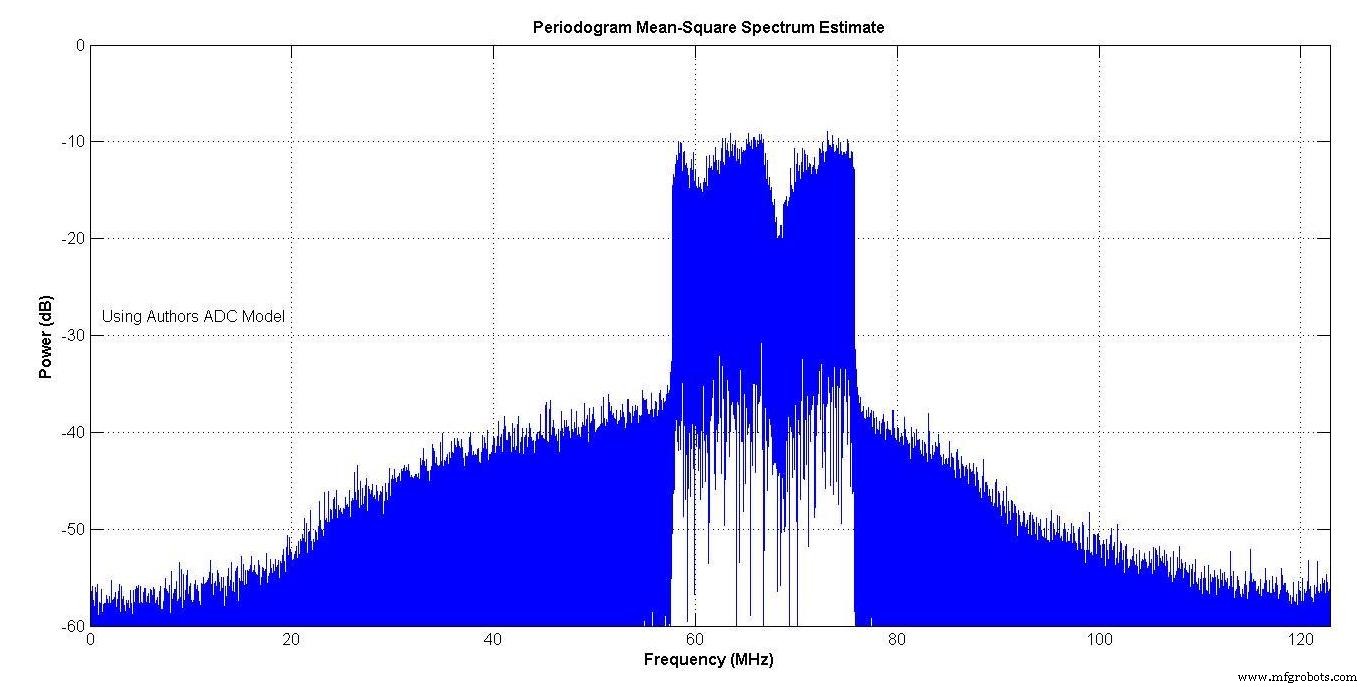
Figuur 14.

Afbeelding 15 toont de constellatie van de ontvangen OFDM voor het model van de fabrikant en Afbeelding 16 toont deze voor het model van uw auteur.

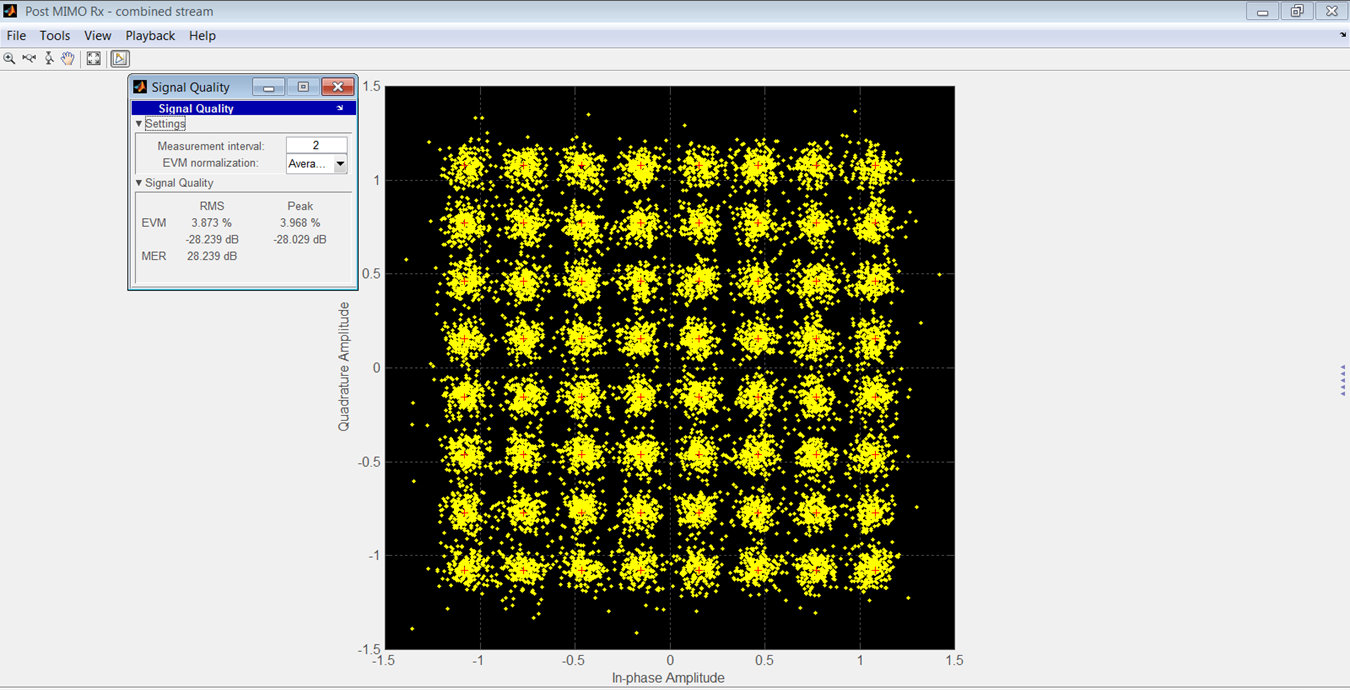
Figuur 15.

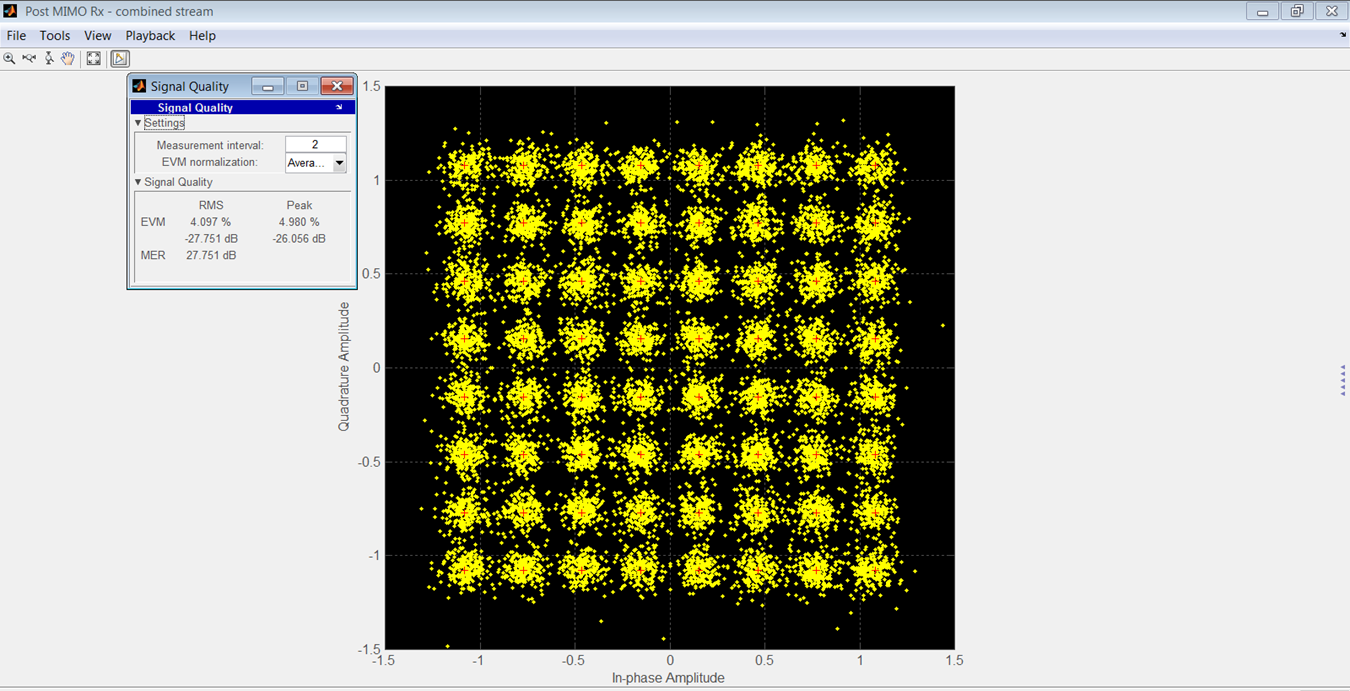
Figuur 16.

Een vergelijking van rms en piek-EVM's staat in tabel 3. De SNR was 90 dB voor deze resultaten.

Tabel 3.

Over een bereik van -7 tot -47 dBrmsFS was het rms-verschil tussen EVM's van de twee modellen 3,46 dB.

Over het algemeen geeft het model van uw auteur zeer vergelijkbare resultaten als dat van de fabrikant, voor een vrij eenvoudige set parameters. Er was geen informatie over het model van de fabrikant beschikbaar, maar deze kan vergelijkbaar zijn met die van uw auteur.

In ieder geval verliepen de simulaties sneller bij gebruik van uw auteursmodel, omdat het niet nodig was om gegevens tussen simulatiesoftware over te dragen. Het model van uw auteur is dus gebruikt in de bit error rate (BER)-simulatie die wordt getoond in Afbeelding 17.

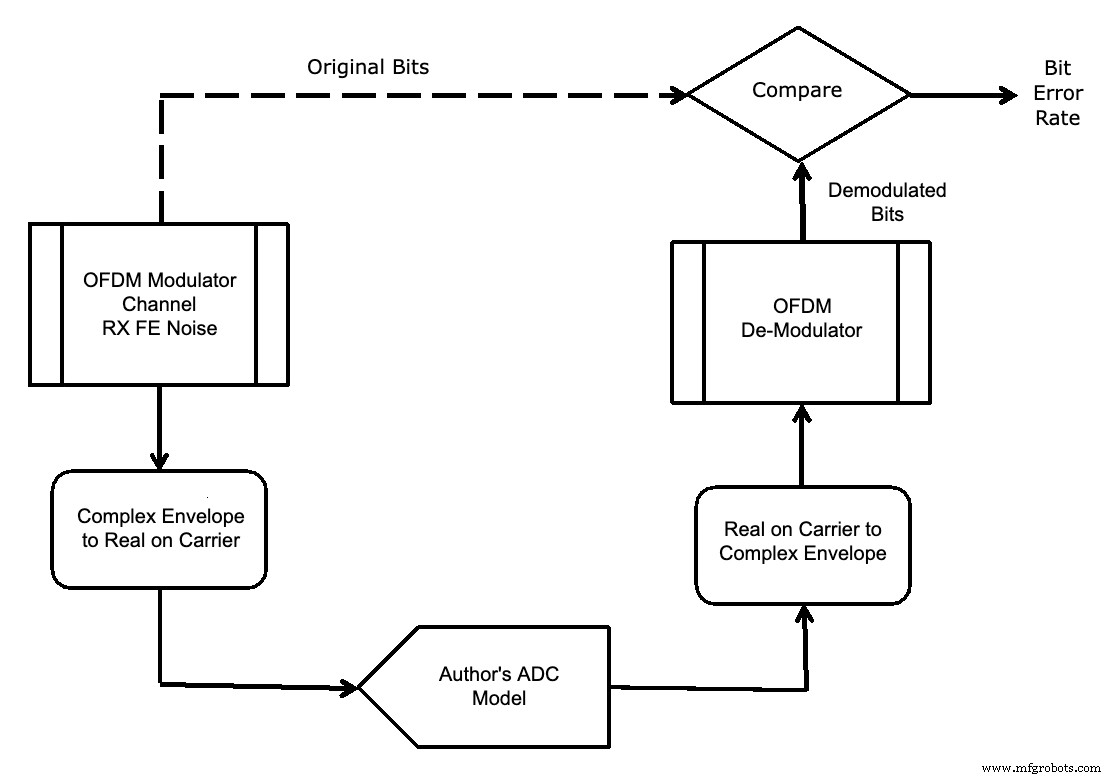
Figuur 17.

Een belangrijke parameter bij het ontwerpen van een systeem met een ADC is het optimale niveau om het signaal te plaatsen ten opzichte van de volledige schaal van de ADC.

Een te laag niveau resulteert in een te klein signaal ten opzichte van de ruis en vervorming.

Een te hoog niveau resulteert in overmatige clipping, wat ook het signaal vervormt. Gewoonlijk is een niveau dat enige clipping mogelijk maakt optimaal.

De BER voor drie verschillende SNR's en signaalniveaus van -41 tot -7 dBrmsFS wordt weergegeven in afbeelding 18.

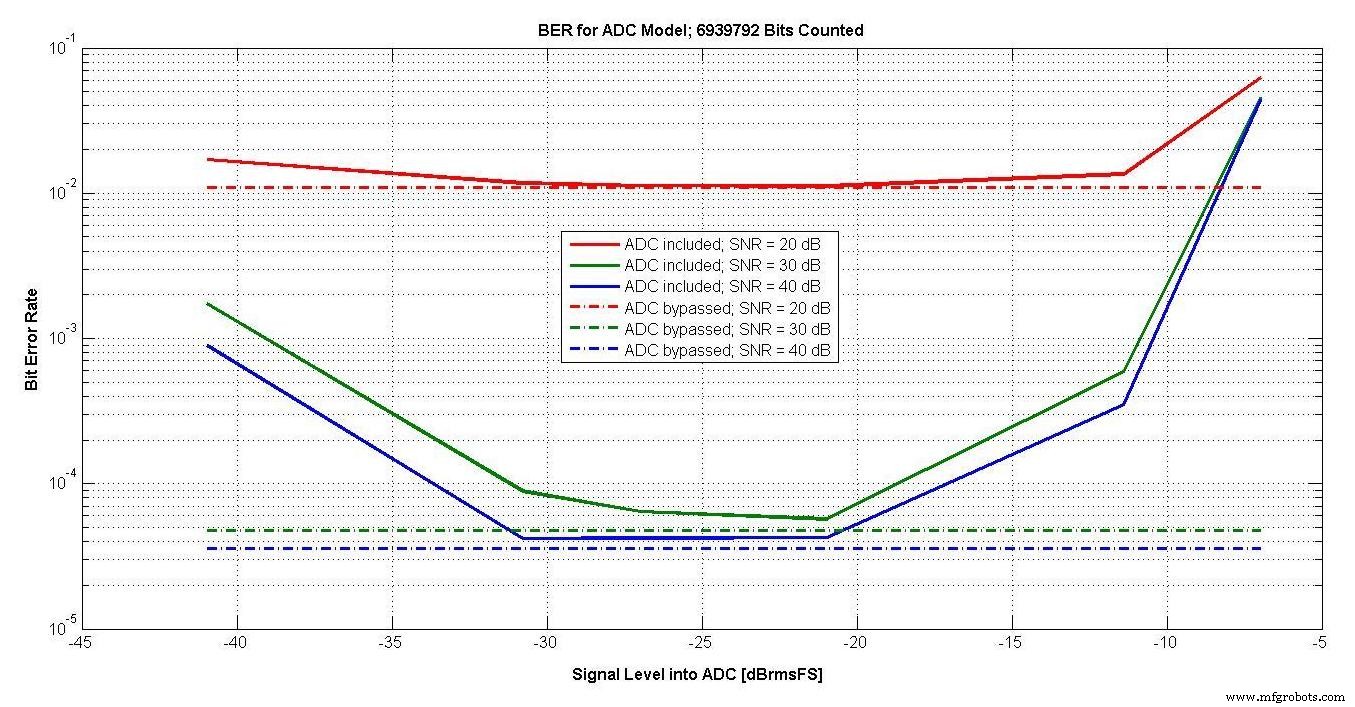
Figuur 18.

Ook weergegeven met de stippellijnen is de BER wanneer het ADC-model wordt omzeild. Met de ADC is er een bereik van ongeveer 10 dB dat optimaal is, en een automatische versterkingsregeling zou het signaal in dit bereik moeten houden.

In het volgende artikel zullen we deze serie afsluiten met enkele gedachten over een beter te gebruiken model en ook wat te praten over modellen voor DAC's. Deel uw mening over deze serie in de onderstaande opmerkingen.