Neurale netwerkarchitectuur voor een Python-implementatie

Dit artikel bespreekt de Perceptron-configuratie die we zullen gebruiken voor onze experimenten met training en classificatie van neurale netwerken, en we zullen ook kijken naar het verwante onderwerp van bias-knooppunten.

Welkom bij de reeks technische artikelen over neurale netwerken van All About Circuits. In de serie tot nu toe - die hieronder is gelinkt - hebben we behoorlijk wat theorie over neurale netwerken behandeld.

1. Hoe classificatie uitvoeren met behulp van een neuraal netwerk:wat is de Perceptron?
2. Een eenvoudig Perceptron neuraal netwerkvoorbeeld gebruiken om gegevens te classificeren
3. Een basis Perceptron neuraal netwerk trainen
4. Eenvoudige neurale netwerktraining begrijpen
5. Een inleiding tot trainingstheorie voor neurale netwerken
6. De leersnelheid in neurale netwerken begrijpen
7. Geavanceerde machine learning met de meerlaagse Perceptron
8. De Sigmoid-activeringsfunctie:activering in meerlaagse Perceptron neurale netwerken
9. Een meerlagig Perceptron neuraal netwerk trainen
10. Trainingsformules en backpropagation voor meerlaagse perceptrons begrijpen
11. Neurale netwerkarchitectuur voor een Python-implementatie
12. Hoe maak je een meerlaags Perceptron neuraal netwerk in Python
13. Signaalverwerking met behulp van neurale netwerken:validatie in neuraal netwerkontwerp
14. Trainingsdatasets voor neurale netwerken:een neuraal netwerk met Python trainen en valideren

Nu zijn we klaar om deze theoretische kennis om te zetten in een functioneel Perceptron-classificatiesysteem.

Eerst wil ik de algemene kenmerken van het netwerk introduceren die we zullen implementeren in een programmeertaal op hoog niveau; Ik gebruik Python, maar de code zal worden geschreven op een manier die vertaling naar andere talen zoals C vergemakkelijkt. Het volgende artikel geeft de gedetailleerde uitleg van de Python-code, en daarna zullen we verschillende manieren van trainen verkennen , gebruiken en evalueren van dit netwerk.

De Python neurale netwerkarchitectuur

De software komt overeen met de Perceptron afgebeeld in het volgende diagram.

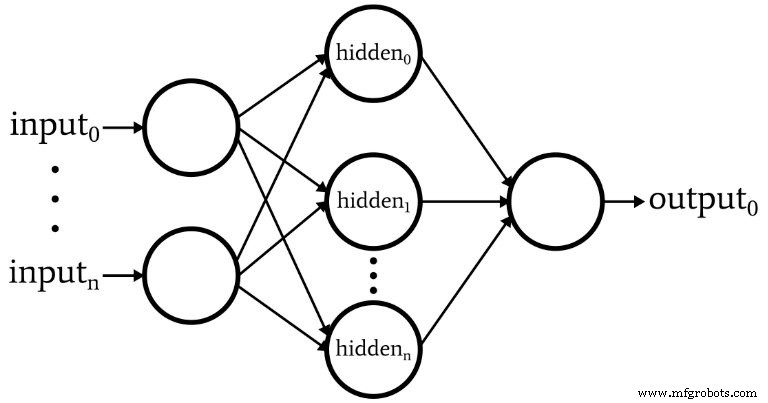
Dit zijn de basiskenmerken van het netwerk:

• Het aantal invoerknooppunten is variabel. Dit is essentieel als we een netwerk willen dat enige mate van flexibiliteit heeft, omdat de invoerdimensionaliteit moet overeenkomen met de dimensionaliteit van de monsters die we willen classificeren.
• De code ondersteunt niet meerdere verborgen lagen. Op dit moment is dat niet nodig:één verborgen laag is genoeg voor een extreem krachtige classificatie.
• Het aantal knooppunten binnen de ene verborgen laag is variabel. Het vinden van het optimale aantal verborgen knooppunten vereist wat vallen en opstaan, hoewel er richtlijnen zijn die ons kunnen helpen een redelijk startpunt te kiezen. In een toekomstig artikel zullen we het probleem van de verborgen laag-dimensionaliteit onderzoeken.
• Het aantal uitvoerknooppunten is momenteel vastgesteld op één. Deze beperking zal ons aanvankelijke programma een beetje eenvoudiger maken en we kunnen variabele uitvoerdimensionaliteit opnemen in een verbeterde versie.
• De activeringsfunctie voor zowel verborgen als uitvoerknooppunten is de standaard logistieke sigmoid-relatie:

\[f(x)=\frac{1}{1+e^{-x}}\]

Wat is een bias-knooppunt? (AKA Bias is goed als je een Perceptron bent)

Terwijl we het hebben over netwerkarchitectuur, moet ik erop wijzen dat neurale netwerken vaak iets bevatten dat een bias-knooppunt wordt genoemd (of je kunt het gewoon een 'bias' noemen, zonder 'knooppunt'). De numerieke waarde die is gekoppeld aan een bias-knooppunt is een constante gekozen door de ontwerper. Bijvoorbeeld:

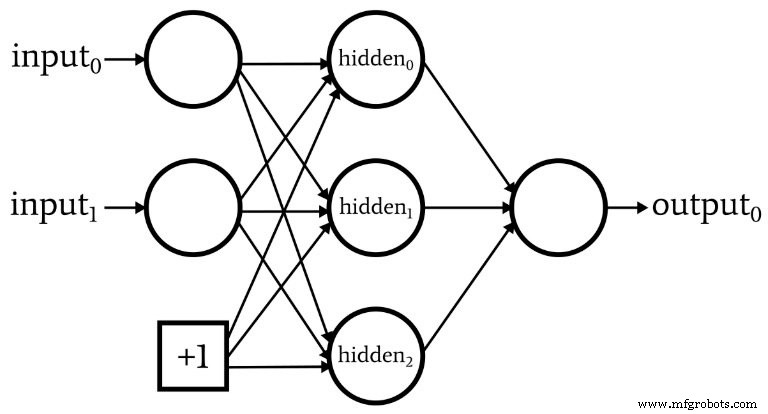
Bias-knooppunten kunnen worden opgenomen in de invoerlaag of de verborgen laag, of beide. Hun gewichten zijn net als alle andere gewichten en worden bijgewerkt met dezelfde backpropagation-procedure.

Het gebruik van bias-knooppunten is een belangrijke reden om neurale netwerkcode te schrijven waarmee u eenvoudig het aantal invoerknooppunten of verborgen knooppunten kunt wijzigen, zelfs als u alleen geïnteresseerd bent in één specifieke classificatietaak, variabele invoer- en verborgen laagdimensionaliteit zorgt ervoor dat u gemakkelijk kunt experimenteren met het gebruik van bias-knooppunten.

In deel 10 heb ik erop gewezen dat het preactiveringssignaal van een knooppunt wordt berekend door een puntproduct uit te voeren, d.w.z. je vermenigvuldigt de overeenkomstige elementen van twee arrays (of vectoren, als je dat liever hebt) en telt vervolgens alle afzonderlijke producten bij elkaar op. De eerste array bevat de waarden na activering van de voorgaande laag en de tweede array bevat de gewichten die de voorgaande laag met de huidige laag verbinden. Als de postactivatie-array van de voorgaande laag dus wordt aangegeven met x en de gewichtsvector wordt aangegeven met w, wordt een preactiveringswaarde als volgt berekend:

\[S_{preA} =w \cdot x =sum(w_1x_1 + w_2x_2 + \cdots + w_nx_n)\]

Je vraagt ​​je misschien af ​​wat dit in hemelsnaam met bias-knooppunten te maken heeft. Welnu, de bias (aangeduid met b) wijzigt deze procedure als volgt:

\[S_{preA} =( w \cdot x)+b =sum(w_1x_1 + w_2x_2 + \cdots + w_nx_n)+b\]

Een bias verschuift het signaal dat wordt verwerkt door de activeringsfunctie en kan daardoor het netwerk flexibeler en robuuster maken. Het gebruik van de letter b om de biaswaarde aan te duiden doet denken aan het "y-snijpunt" in de standaardvergelijking voor een rechte lijn:y =mx + b . En dit is geen ijdel toeval. De bias is inderdaad als een y-snijpunt, en je hebt misschien ook gemerkt dat de reeks gewichten gelijk is aan een helling:

\[S_{preA} =( w \cdot x)+b\]

\[y =mx + b\]

Gewichten, bias en activering

Als we nadenken over de numerieke waarden die tijdens de training aan de activeringsfunctie van een knooppunt worden geleverd, verhogen of verlagen de gewichten de helling van de invoergegevens en verschuift de bias de invoergegevens verticaal. Maar hoe beïnvloedt dit de uitvoer van het knooppunt? Laten we aannemen dat we de standaard logistische functie gebruiken voor activering:

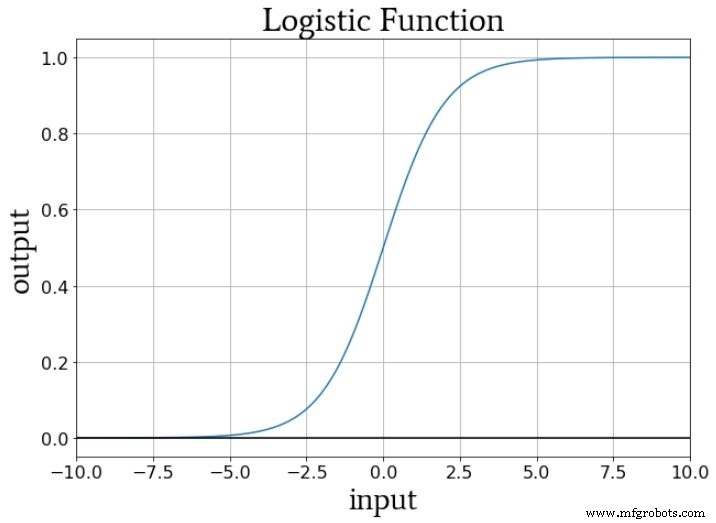
De overgang van f_A (x) =0 tot f_A (x) =1 is gecentreerd op een invoerwaarde van x =0. Dus door een bias te gebruiken om het preactiveringssignaal te verhogen of te verlagen, kunnen we het optreden van de overgang beïnvloeden en daardoor de activeringsfunctie naar links of rechts verschuiven . De gewichten daarentegen bepalen hoe "snel" de invoerwaarde door x =0 gaat, en dit beïnvloedt de steilheid van de overgang in de activeringsfunctie.

Conclusie

We hebben bias-knooppunten en de meest opvallende kenmerken van het eerste neurale netwerk besproken dat we in software zullen implementeren. Nu zijn we klaar om naar de eigenlijke code te kijken, en dat is precies wat we in het volgende artikel zullen doen.