Reliability Engineering Principles for the Plant Engineer

Steeds vaker nemen managers en ingenieurs die verantwoordelijk zijn voor productie en andere industriële activiteiten een focus op betrouwbaarheid op in hun strategische en tactische plannen en initiatieven. Deze trend is van invloed op tal van functionele gebieden, waaronder ontwerp en inkoop van machines/systemen, fabrieksoperaties en fabrieksonderhoud.

Met zijn oorsprong in de luchtvaartindustrie, was betrouwbaarheidsengineering als discipline van oudsher voornamelijk gericht op het verzekeren van productbetrouwbaarheid. Deze methoden worden steeds vaker gebruikt om de productiebetrouwbaarheid van fabrieken en apparatuur te waarborgen, vaak als een hulpmiddel voor lean manufacturing. Dit artikel biedt een inleiding tot de meest relevante en praktische van deze methoden voor de engineering van fabrieksbetrouwbaarheid, waaronder:

• Basisbetrouwbaarheidsberekeningen voor uitvalpercentage, MTBF, beschikbaarheid, enz.
• Een inleiding tot de exponentiële verdeling - de hoeksteen van de betrouwbaarheidsmethoden.
• Identificeren van faaltijdafhankelijkheden met behulp van het veelzijdige Weibull-systeem.
• Ontwikkelen van een effectief systeem voor het verzamelen van veldgegevens.

Geschiedenis van betrouwbaarheidstechniek

De oorsprong van het vakgebied van de betrouwbaarheidstechniek, althans de vraag ernaar, gaat terug tot het punt waarop de mens voor zijn levensonderhoud afhankelijk begon te worden van machines. De Noria is bijvoorbeeld een oude pomp waarvan wordt gedacht dat het de eerste geavanceerde machine ter wereld is. Gebruikmakend van hydraulische energie uit de stroming van een rivier of beek, gebruikten de Noria emmers om water over te brengen naar troggen, viaducten en andere distributieapparatuur om velden te irrigeren en gemeenschappen van water te voorzien.

Als de gemeenschap Noria faalde, liepen de mensen die ervan afhankelijk waren voor hun voedselvoorziening gevaar. Overleven is altijd een grote bron van motivatie geweest voor betrouwbaarheid en betrouwbaarheid.

Hoewel de oorsprong van de vraag oud is, bloeide betrouwbaarheidstechniek als een technische discipline echt op, samen met de groei van de commerciële luchtvaart na de Tweede Wereldoorlog. Het werd al snel duidelijk voor managers van bedrijven in de luchtvaartindustrie dat crashes slecht zijn voor de zaken. Karen Bernowski, redacteur van Quality Progress , onthulde in een van haar hoofdartikelen onderzoek naar de mediawaarde van de dood op verschillende manieren, dat werd uitgevoerd door MIT-hoogleraar statistiek Arnold Barnett en gerapporteerd in 1994.

Barnett evalueerde op verschillende manieren het aantal voorpaginanieuwsartikelen van de New York Times per 1.000 doden. Hij ontdekte dat aan kanker gerelateerde sterfgevallen 0,02 voorpaginanieuws opleverden per 1000 doden, moord op 1,7 op 1000 doden, aids op 2,3 op 1000 doden en luchtvaartgerelateerde ongevallen leverden maar liefst 138,2 artikelen op per 1000 doden!

De kosten en het opvallende karakter van luchtvaartgerelateerde ongevallen hebben de luchtvaartindustrie ertoe aangezet om sterk deel te nemen aan de ontwikkeling van de discipline betrouwbaarheidstechniek. Evenzo, vanwege de kritieke aard van militair materieel in de defensie, zijn technieken voor betrouwbaarheidsengineering al lang gebruikt om operationele paraatheid te verzekeren. Veel van onze normen op het gebied van betrouwbaarheidsengineering zijn MIL-normen of hebben hun oorsprong in militaire activiteiten.

Wat is Reliability Engineering?

Reliability engineering houdt zich bezig met de levensduur en betrouwbaarheid van onderdelen, producten en systemen. Wat nog schrijnender is, gaat over het beheersen van risico's. Reliability engineering omvat een breed scala aan analytische technieken die zijn ontworpen om ingenieurs te helpen de storingsmodi en patronen van deze onderdelen, producten en systemen te begrijpen. Traditioneel was het vakgebied van de betrouwbaarheidsengineering gericht op productbetrouwbaarheid en betrouwbaarheidsgarantie.

In de afgelopen jaren zijn organisaties die machines en andere fysieke activa in productieomgevingen inzetten, begonnen met het implementeren van verschillende principes voor betrouwbaarheidsengineering met het oog op productiebetrouwbaarheid en betrouwbaarheidsborging.

Productieorganisaties passen steeds vaker technieken voor betrouwbaarheidsengineering toe, zoals Reliability-Centered Maintenance (RCM), inclusief storingsmodi en effecten (en kriticiteits)analyse (FMEA, FMECA), root cause analysis (RCA), condition-based onderhoud, verbeterde werkplanningsschema's, enz. Deze zelfde organisaties beginnen op levenscycluskosten gebaseerde ontwerp- en inkoopstrategieën, wijzigingsbeheerschema's en andere geavanceerde tools en technieken toe te passen om de grondoorzaken van slechte betrouwbaarheid onder controle te krijgen.

De acceptatie van de meer kwantitatieve aspecten van betrouwbaarheidsengineering door de gemeenschap van productiebetrouwbaarheidsborging verliep echter traag. Dit komt deels door de waargenomen complexiteit van de technieken en deels door de moeilijkheid om bruikbare gegevens te verkrijgen.

De kwantitatieve aspecten van betrouwbaarheidsengineering lijken op het eerste gezicht misschien ingewikkeld en ontmoedigend. In werkelijkheid kan een relatief basaal begrip van de meest fundamentele en breed toepasbare methoden de betrouwbaarheidsingenieur van de fabriek echter in staat stellen een veel beter begrip te krijgen van waar problemen zich voordoen, hun aard en hun impact op het productieproces - althans in de kwantitatieve zin.

Als ze op de juiste manier worden gebruikt, stellen de tools en methoden voor kwantitatieve betrouwbaarheidsengineering de fabrieksbetrouwbaarheidsengineering in staat om de kaders van RCM, RCA, enz. Ingenieurs moeten echter bijzonder slim zijn in het toepassen van de methoden.

Waarom? De operationele context en omgeving van een productieproces omvat meer variabelen dan de enigszins eendimensionale wereld van productbetrouwbaarheidsgarantie. Dit komt door de gecombineerde invloed van ontwerptechniek, inkoop, productie/operaties, onderhoud, enz., en de moeilijkheid om effectieve tests en experimenten te maken om de multidimensionale aspecten van een typische productieomgeving te modelleren.

Ondanks de toegenomen moeilijkheid bij het toepassen van kwantitatieve betrouwbaarheidsmethoden in de productieomgeving, is het niettemin de moeite waard om de tools goed te begrijpen en waar nodig toe te passen. Kwantitatieve gegevens helpen bij het bepalen van de aard en omvang van een probleem/kans, wat inzicht geeft in de betrouwbaarheid in zijn of haar toepassing van andere tools voor betrouwbaarheidsengineering.

Dit artikel biedt een inleiding tot de meest elementaire methoden voor betrouwbaarheidsengineering die van toepassing zijn op de fabrieksingenieur die geïnteresseerd is in productiebetrouwbaarheidsborging. Het veronderstelt een basiskennis van algebra, waarschijnlijkheidstheorie en univariate statistieken op basis van de Gaussische (normale) verdeling (bijv. maat voor centrale tendens, maten voor spreiding en variabiliteit, betrouwbaarheidsintervallen, enz.).

Het moet duidelijk worden gemaakt dat dit document een korte inleiding is tot betrouwbaarheidsmethoden. Het is geenszins een uitgebreid overzicht van methoden voor betrouwbaarheidsengineering, en het is op geen enkele manier nieuw of onconventioneel. De hierin beschreven methoden worden routinematig gebruikt door betrouwbaarheidsingenieurs en zijn kernkennisconcepten voor diegenen die professionele certificering nastreven door de American Society for Quality (ASQ) als betrouwbaarheidsingenieur (CRE).

In de bibliografie van dit artikel staan ​​verschillende boeken over betrouwbaarheidstechniek vermeld. De auteur van dit artikel heeft gevonden Betrouwbaarheidsmethoden voor ingenieurs door KS Krishnamoorthi en Betrouwbaarheidsstatistieken door Robert Dovich als bijzonder nuttige en gebruiksvriendelijke referenties op het gebied van methoden voor betrouwbaarheidsengineering. Beide worden gepubliceerd door de ASQ Press.

Voordat u methoden bespreekt, dient u vertrouwd te raken met de nomenclatuur van de betrouwbaarheidstechniek. Voor het gemak vindt u in de bijlage van dit artikel een zeer beknopte lijst met belangrijke termen en definities. Raadpleeg MIL-STD-721 en andere gerelateerde normen voor een meer uitputtende definitie van betrouwbaarheidstermen en nomenclatuur. De definities in de bijlage zijn van MIL-STD-721.

Wiskundige basisconcepten in Reliability Engineering

Veel wiskundige concepten zijn van toepassing op betrouwbaarheidsengineering, met name op het gebied van waarschijnlijkheid en statistiek. Evenzo kunnen veel wiskundige verdelingen voor verschillende doeleinden worden gebruikt, waaronder de Gaussische (normale) verdeling, de log-normale verdeling, de Rayleigh-verdeling, de exponentiële verdeling, de Weibull-verdeling en tal van andere.

Voor deze korte inleiding zullen we onze discussie beperken tot de exponentiële verdeling en de Weibull-verdeling, de twee die het meest worden toegepast op betrouwbaarheidsengineering. In het belang van de beknoptheid en eenvoud zijn belangrijke wiskundige concepten zoals distributie goodness-of-fit en betrouwbaarheidsintervallen uitgesloten.

Faalpercentage en gemiddelde tijd tussen/tot falen (MTBF/MTTF)

Het doel van kwantitatieve betrouwbaarheidsmetingen is om de faalkans te definiëren in relatie tot de tijd en om die faalkans te modelleren in een wiskundige verdeling met als doel de kwantitatieve aspecten van falen te begrijpen. De meest elementaire bouwsteen is het faalpercentage, dat wordt geschat met behulp van de volgende vergelijking:

Waar:
λ =Mislukkingspercentage (soms aangeduid als het risicopercentage)
T =Totale looptijd/cycli/mijlen/etc. tijdens een onderzoeksperiode voor zowel mislukte als niet-gefaalde items.
r =Het totale aantal storingen tijdens de onderzoeksperiode.

Als bijvoorbeeld vijf elektromotoren samen in totaal 50 jaar in bedrijf zijn met vijf functionele storingen in de periode, is het uitvalpercentage 0,1 uitval per jaar.

Een ander heel basaal concept is de gemiddelde tijd tussen/tot falen (MTBF/MTTF). Het enige verschil tussen MTBF en MTTF is dat we MTBF gebruiken bij het verwijzen naar items die worden gerepareerd als ze defect raken. Voor items die simpelweg worden weggegooid en vervangen, gebruiken we de term MTTF. De berekeningen zijn hetzelfde.

De basisberekening om de gemiddelde tijd tussen falen (MTBF) en gemiddelde tijd tot falen (MTTF) te schatten, beide maten van centrale tendens, is eenvoudigweg het omgekeerde van de functie voor het percentage mislukkingen. Het wordt berekend met behulp van de volgende vergelijking.

Waar:
θ =Gemiddelde tijd tussen/tot falen
T =Totale looptijd/cycli/mijlen/etc. tijdens een onderzoeksperiode voor zowel mislukte als niet-gefaalde items.
r =Het totale aantal storingen tijdens de onderzoeksperiode.

De MTBF voor ons voorbeeld van een industriële elektromotor is 10 jaar, wat het omgekeerde is van het uitvalpercentage voor de motoren. Overigens zouden we MTBF schatten voor elektromotoren die bij storing worden herbouwd. Voor kleinere motoren die als wegwerpmotoren worden beschouwd, zouden we de mate van centrale tendens als MTTF aangeven.

Het uitvalpercentage is een basiscomponent van veel complexere betrouwbaarheidsberekeningen. Afhankelijk van het mechanische/elektrische ontwerp, de bedrijfscontext, de omgeving en/of de effectiviteit van het onderhoud, kan het uitvalpercentage van een machine als functie van de tijd afnemen, constant blijven, lineair toenemen of geometrisch toenemen (Figuur 1). Het belang van faalpercentage versus tijd zal later in meer detail worden besproken.

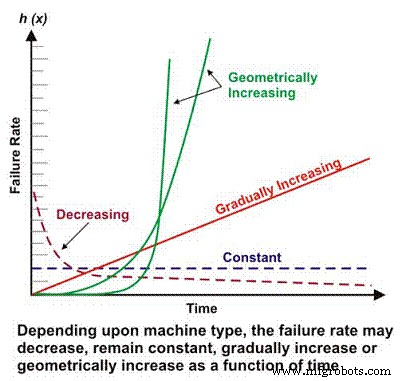
Figuur 1. Verschillende uitvalpercentages versus tijdscenario's

De 'Badkuip'-curve

Personen die alleen een basisopleiding in kansrekening en statistiek hebben gevolgd, zijn waarschijnlijk het meest bekend met de Gauss- of normale verdeling, die wordt geassocieerd met de bekende klokvormige kansdichtheidscurve. De Gauss-verdeling is algemeen toepasbaar op datasets waar de twee meest voorkomende maten van centrale tendens, gemiddelde en mediaan, ongeveer gelijk zijn.

Verrassend genoeg is het, ondanks de veelzijdigheid van de Gauss-verdeling bij het modelleren van kansen voor fenomenen variërend van gestandaardiseerde testscores tot het geboortegewicht van baby's, niet de dominante verdeling die wordt gebruikt in betrouwbaarheidstechniek. De Gauss-verdeling heeft zijn plaats bij het evalueren van de faalkenmerken van machines met een dominante faalmodus, maar de primaire verdeling die wordt gebruikt in betrouwbaarheidsengineering is de exponentiële verdeling.

Bij het evalueren van de betrouwbaarheid en faalkenmerken van een machine, moeten we beginnen met de veel verguisde "badkuip" -curve, die het faalpercentage versus de tijd weerspiegelt (Figuur 2). In concept demonstreert de badkuipcurve effectief de drie fundamentele faalkarakteristieken van een machine:afnemend, constant of toenemend. Helaas is de badkuipcurve fel bekritiseerd in de literatuur over onderhoudstechniek omdat het er niet in slaagt om het karakteristieke uitvalpercentage voor de meeste machines in een industriële fabriek effectief te modelleren, wat over het algemeen geldt op macroniveau.

De meeste machines brengen hun leven door in het vroege leven, of kindersterfte, en/of de constante uitvalpercentages van de badkuipcurve. We zien zelden systemische, op tijd gebaseerde storingen in industriële machines. Ondanks zijn beperkingen bij het modelleren van de uitvalpercentages van typische industriële machines, is de badkuipcurve een handig hulpmiddel om de basisconcepten van betrouwbaarheidsengineering uit te leggen.

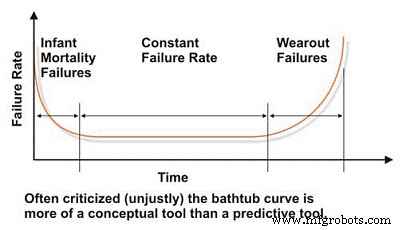
Figuur 2. De veel verguisde 'badkuip'-curve

Het menselijk lichaam is een uitstekend voorbeeld van een systeem dat de badkuipcurve volgt. Mensen, en andere organische soorten trouwens, hebben de neiging om tijdens hun eerste levensjaren, vooral de eerste jaren, een hoog percentage mislukkingen (sterfte) te hebben, maar dit percentage neemt af naarmate het kind ouder wordt. Ervan uitgaande dat een persoon de puberteit bereikt en zijn of haar tienerjaren overleeft, wordt zijn of haar sterftecijfer redelijk constant en blijft daar totdat leeftijds- (tijds)afhankelijke ziekten het sterftecijfer beginnen te verhogen (slijtage).

Talloze invloeden zijn van invloed op sterftecijfers, waaronder prenatale zorg en voeding van de moeder, kwaliteit en beschikbaarheid van medische zorg, omgeving en voeding, levensstijlkeuzes en natuurlijk genetische aanleg. Deze factoren kunnen metaforisch worden vergeleken met factoren die de levensduur van machines beïnvloeden. Ontwerp en aanschaf is analoog aan genetische aanleg; installatie en inbedrijfstelling is analoog aan prenatale zorg en moedervoeding; en levensstijlkeuzes en beschikbaarheid van medische zorg zijn analoog aan de effectiviteit van onderhoud en proactieve controle over de bedrijfsomstandigheden.

De exponentiële verdeling

De exponentiële verdeling, de meest basale en meest gebruikte betrouwbaarheidsvoorspellingsformule, modelleert machines met het constante uitvalpercentage of het vlakke gedeelte van de badkuipcurve. De meeste industriële machines brengen het grootste deel van hun leven door in het constante uitvalpercentage, dus het is breed toepasbaar. Hieronder vindt u de basisvergelijking voor het schatten van de betrouwbaarheid van een machine die de exponentiële verdeling volgt, waarbij het uitvalpercentage constant is als functie van de tijd.

Waar:
R(t) =Betrouwbaarheidsschatting voor een periode, cycli, mijlen, etc. (t).
e =Basis van de natuurlijke logaritmen (2,718281828)
λ =Foutpercentage (1/MTBF of 1/MTTF)

Als u in ons voorbeeld van een elektrische motor uitgaat van een constant storingspercentage, is de kans dat een motor zes jaar zonder storing loopt, of de verwachte betrouwbaarheid, 55 procent. Dit wordt als volgt berekend:
R(6) =2,718281828-(0,1* 6)
R(6) =0,5488 =~ 55%

Met andere woorden, na zes jaar kan worden verwacht dat ongeveer 45% van de populatie identieke motoren die in een identieke toepassing werken, faalt. Het is de moeite waard om op dit punt te herhalen dat deze berekeningen de waarschijnlijkheid voor een populatie projecteren. Elk individu uit de populatie zou kunnen falen op de eerste dag van de operatie, terwijl een ander individu het 30 jaar zou kunnen volhouden. Dat is de aard van probabilistische betrouwbaarheidsprojecties.

Een kenmerk van de exponentiële verdeling is dat de MTBF optreedt op het punt waarop de berekende betrouwbaarheid 36,78% is, of het punt waarop 63,22% van de machines al is uitgevallen. In ons motorvoorbeeld kan worden verwacht dat na 10 jaar 63,22% van de motoren uit een populatie van identieke motoren die in identieke toepassingen worden gebruikt, zullen falen. Met andere woorden, het overlevingspercentage is 36,78% van de bevolking.

We spreken vaak van geprojecteerde levensduur van de lagers als de L10-levensduur. Dit is het moment waarop verwacht mag worden dat 10% van een populatie lagers faalt (overlevingspercentage van 90%). In werkelijkheid overleeft slechts een fractie van de lagers het L10-punt. We zijn dat gaan accepteren als de objectieve levensduur van een peiling, terwijl we misschien onze zinnen moeten zetten op het L63.22-punt, wat aangeeft dat onze peilingen gemiddeld langer meegaan dan de verwachte MTBF – uiteraard in de veronderstelling dat de peilingen volg de exponentiële verdeling. We zullen dat probleem later bespreken in de Weibull-analysesectie van het artikel.

De kansdichtheidsfunctie (pdf), of levensduurverdeling, is een wiskundige vergelijking die de faalfrequentieverdeling benadert. Het is de pdf, of levensfrequentieverdeling, die de bekende klokvormige curve in de Gaussische of normale verdeling oplevert. Hieronder staat de pdf voor de exponentiële verdeling.

Waar:
pdf(t) =Levensfrequentieverdeling voor een bepaalde tijd (t)
e =Basis van de natuurlijke logaritmen (2,718281828)
λ =Foutpercentage (1/MTBF of 1/MTTF)

In ons voorbeeld van een elektromotor wordt de werkelijke faalkans na drie jaar als volgt berekend:
pdf(3) =01. * 2.718281828-(0.1* 3)
pdf(3) =0.1 * 0.7408
pdf(3) =0,07408 =~ 7,4%

Als we in ons voorbeeld uitgaan van een constant uitvalpercentage, dat de exponentiële verdeling volgt, wordt de levensduurverdeling of pdf voor de industriële elektromotoren uitgedrukt in figuur 3. Laat u niet verwarren door de afnemende aard van de pdf-functie. Ja, het percentage mislukkingen is constant, maar de pdf gaat wiskundig uit van een storing zonder vervanging, dus de populatie waaruit storingen kunnen optreden neemt voortdurend af - asymptotisch bijna nul.

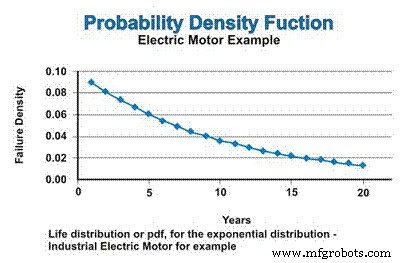
Figuur 3. De kansdichtheidsfunctie (pdf)

De cumulatieve distributiefunctie (cdf) is gewoon het cumulatieve aantal storingen dat men over een bepaalde periode zou kunnen verwachten. Voor de exponentiële verdeling is het uitvalpercentage constant, dus de relatieve snelheid waarmee defecte componenten aan de cdf worden toegevoegd, blijft constant. Echter, naarmate de populatie afneemt als gevolg van falen, neemt het werkelijke aantal wiskundig geschatte mislukkingen af ​​als functie van de afnemende populatie. Net zoals de pdf asymptotisch nul nadert, nadert de cdf asymptotisch één (Figuur 4).

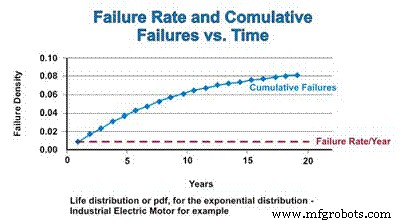
Figuur 4. Foutpercentage en de cumulatieve distributiefunctie

Het afnemende faalpercentage van de badkuipcurve, dat vaak het gebied van de kindersterfte wordt genoemd, en het slijtagegebied zullen worden besproken in de volgende sectie over de veelzijdige Weibull-verdeling.

Weibull-distributie

Oorspronkelijk ontwikkeld door Wallodi Weibull, een Zweedse wiskundige, is de Weibull-analyse verreweg de meest veelzijdige distributie die wordt gebruikt door betrouwbaarheidsingenieurs. Hoewel het een distributie wordt genoemd, is het in feite een hulpmiddel waarmee de betrouwbaarheidsingenieur eerst de kansdichtheidsfunctie (storingsfrequentieverdeling) van een set storingsgegevens kan karakteriseren om de storingen te karakteriseren als vroege levensduur, constant (exponentieel) of slijtage. (Gaussiaans of log-normaal) door de tijd tot falen uit te zetten op een speciaal plotpapier met de log van de tijden/cycli/mijlen tot falen, een log geschaalde X-as uitgezet tegen het cumulatieve percentage van de populatie vertegenwoordigd door elke storing op een log -log geschaalde Y-as (Figuur 5).

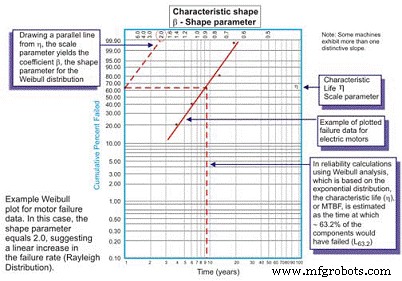
Figuur 5. De eenvoudige Weibull-plot – geannoteerd

Eenmaal uitgezet, is de lineaire helling van de resulterende curve een belangrijke variabele, de vormparameter genaamd, weergegeven door â, die wordt gebruikt om de exponentiële verdeling aan te passen aan een groot aantal storingsverdelingen. In het algemeen, als de â-coëfficiënt, of vormparameter, kleiner is dan 1,0, vertoont de verdeling mislukkingen in het vroege leven of kindersterfte. Als de vormparameter ongeveer 3,5 overschrijdt, zijn de gegevens tijdsafhankelijk en duiden ze op slijtagefouten.

Deze dataset gaat doorgaans uit van de Gaussische of normale verdeling. Naarmate de â-coëfficiënt boven ~ 3,5 uitkomt, wordt de klokvormige verdeling strakker, met toenemende kurtosis (piek aan de bovenkant van de curve) en een kleinere standaarddeviatie. Veel datasets zullen twee of zelfs drie verschillende regio's vertonen.

Het is gebruikelijk dat betrouwbaarheidsingenieurs bijvoorbeeld één curve plotten die de vormparameter vertegenwoordigt tijdens het inlopen en een andere curve om het constante of geleidelijk toenemende uitvalpercentage weer te geven. In sommige gevallen ontstaat er een derde duidelijke lineaire helling om een ​​derde vorm te identificeren, het slijtagegebied.

In deze gevallen nemen de pdf van de faalgegevens inderdaad de bekende vorm van de badkuipcurve aan (Figuur 6). De meeste mechanische apparatuur die in planten wordt gebruikt, vertoont echter een kindersterftegebied en een constant of geleidelijk toenemend faalpercentage. Het is zeldzaam om een ​​curve te zien die slijtage vertegenwoordigt. De karakteristieke levensduur, of η (kleine letters Grieks "Eta"), is de Weibull-benadering van de MTBF. Het is altijd de functie van tijd, mijlen of cycli waarbij 63,21% van de geëvalueerde eenheden is mislukt, wat de MTBF/MTTF is voor de exponentiële verdeling.

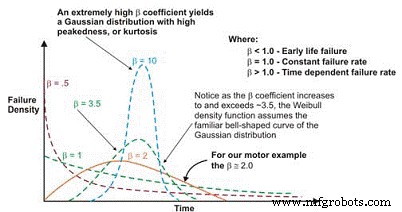
Figuur 6. Afhankelijk van de vormparameter, de Weibull-foutdichtheid curve kan verschillende distributies aannemen, wat het zo veelzijdig maakt voor betrouwbaarheidsengineering.

Als voorbehoud om dit gereedschap terug te koppelen aan uitmuntendheid in onderhoud en operationele uitmuntendheid, als we de forceringsfuncties die leiden tot mechanische storingen in lagers, tandwielen, enz., effectiever zouden beheersen, zoals smering, verontreinigingscontrole, uitlijning, balans, juiste bediening, enz., zouden meer machines daadwerkelijk hun vermoeiingslevensduur bereiken. Machines die hun vermoeiingsleven bereiken, zullen de bekende slijtage-eigenschappen vertonen.

Het gebruik van de β-coëfficiënt om de foutpercentagevergelijking als functie van de tijd aan te passen, levert de volgende algemene vergelijking op:

Waar:
h(t) =Mislukkingspercentage (of risicopercentage) voor een bepaalde tijd (t)
e =Basis van de natuurlijke logaritmen (2,718281828)
θ =Geschatte MTBF/MTTF
β =Weibull-vormparameter uit plot.

En de volgende betrouwbaarheidsfunctie:

Waar:
R(t) =Betrouwbaarheidsschatting voor een periode, cycli, mijlen, enz. (t)
e =Basis van de natuurlijke logaritmen (2,718281828)
θ =Geschatte MTBF/MTTF
β =Weibull-vormparameter uit plot.

En de volgende kansdichtheidsfunctie (pdf):

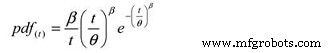
Waar:
pdf(t) =Geschatte kansdichtheidsfunctie voor een tijdsperiode,
cycli, mijlen, enz. (t)
e =Basis van de natuurlijke logaritmen (2,718281828)
θ =Geschatte MTBF/MTTF
β =Weibull-vormparameter uit plot.

Opgemerkt moet worden dat wanneer de β gelijk is aan 1,0, de Weibull-verdeling de vorm aanneemt van de exponentiële verdeling waarop deze is gebaseerd.

Voor niet-ingewijden kan de wiskunde die nodig is om Weibull-analyse uit te voeren, ontmoedigend lijken. Maar als je eenmaal de mechanica van de formules begrijpt, is de wiskunde eigenlijk vrij eenvoudig. Bovendien zal software tegenwoordig het meeste werk voor ons doen, maar het is belangrijk om de onderliggende theorie te begrijpen, zodat de betrouwbaarheidsingenieur van de fabriek de krachtige Weibull-analysetechniek effectief kan inzetten.

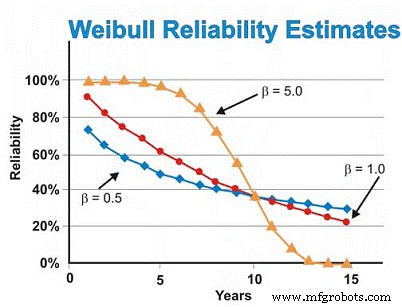
In ons eerder besproken voorbeeld van elektromotoren gingen we eerder uit van de exponentiële verdeling. Als de Weibull-analyse echter mislukkingen in het vroege leven aan het licht bracht door een β-vormparameter van 0,5 op te leveren, zou de schatting van de betrouwbaarheid na zes jaar ~ 46% zijn, niet de ~ 55% geschat uitgaande van de exponentiële verdeling. Om slijtage door slijtage te verminderen, zouden we op onze leveranciers moeten leunen om een ​​beter gebouwde en geleverde kwaliteit en betrouwbaarheid te bieden, de motoren beter op te slaan om roest, corrosie, fretting en andere statische slijtagemechanismen te voorkomen, en een betere installatie van en het opstarten van nieuwe of gereviseerde machines.

Omgekeerd, als Weibull-analyse zou aantonen dat de motoren voornamelijk slijtage-gerelateerde storingen vertoonden, wat een β-vormparameter van 5,0 opleverde, zou de schatting van de betrouwbaarheid na zes jaar ~ 93% zijn, in plaats van de ~ 55% geschat uitgaande van de exponentiële verdeling. Voor tijdsafhankelijke slijtagestoringen kunnen we geplande revisie of vervanging uitvoeren, ervan uitgaande dat we een goede schatting van de MTBF/MTTF hebben nadat we het slijtagegebied hebben bereikt en een voldoende kleine standaarddeviatie om met grote zekerheid beslissingen te nemen over herbouw/vervanging die zijn niet extreem duur.

In ons motorvoorbeeld, uitgaande van een β-vormparameter van 5,0, begint het uitvalpercentage snel te stijgen na ongeveer vijf of zes jaar, dus misschien willen we onze gegevens bewerken om ons alleen te concentreren op het slijtagegebied bij het schatten van op tijd gebaseerde vervanging of herbouw tijd. Als alternatief kunnen we het ontwerp verbeteren, waarbij we ons richten op de dominante faalmodus(en) met als doel het verminderen van "stress-sterkte" interferenties. Met andere woorden, we kunnen proberen de zwakheden van de machine te elimineren door ontwerpaanpassingen, met als doel het elimineren van wat de tijdafhankelijke storingen veroorzaakt.

Ervan uitgaande dat alles constant is, behalve de β-vormparameter, illustreert figuur 7 het verschil dat de β-vormparameter heeft op de schatting van de betrouwbaarheid, uitgaande van β-vormwaarden van 0,5 (vroege levensduur), 1,0 (constant of exponentieel) en 5,0 (slijtage) voor een reeks tijdschattingen. Deze afbeelding illustreert visueel het concept van toenemend risico vs. tijd (β =0,5), constant risico vs. tijd (β =1,0) en toenemend risico vs. tijd (β =5).

Figuur 7. Diverse betrouwbaarheidsprojecties als functie van tijd voor verschillende Weibull-vormparameters

Het Weibull-plot met meerdere hellingen

Vaak is bij het tekenen van een best passende regressielijn door de gegevenspunten op een Weibull-grafiek de correlatiecoëfficiënt slecht, wat betekent dat de werkelijke gegevenspunten een grote afstand van de regressielijn afdwalen. Dit wordt beoordeeld door de correlatiecoëfficiënt R te onderzoeken, of conservatiever, R2, die gegevensvariabiliteit aangeeft. Als de correlatie slecht is, moet de betrouwbaarheidsingenieur de gegevens onderzoeken om te beoordelen of er twee of meer patronen bestaan, wat kan duiden op grote verschillen in faalwijzen, bedrijfscontext, enz. Vaak levert dit twee of meer schattingen van de bèta op (Figuur 8).

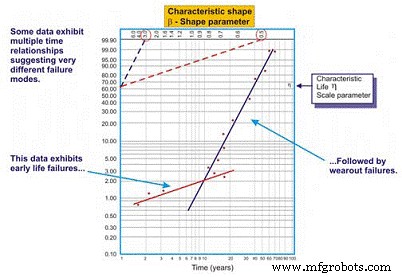
Figuur 8. Een voorbeeld van een Weibull-plot met meerdere bèta's

Zoals we in ons voorbeeld in figuur 8 zien, werkt de dataset beter wanneer twee verschillende regressielijnen worden getekend. De eerste regel vertoont een bètavormparameter van 0,5, wat duidt op mislukkingen in het vroege leven. De tweede regel vertoont een bètavorm van 3,0, wat suggereert dat de kans op falen toeneemt als functie van de tijd. Het is gebruikelijk dat complexe apparatuur, met name mechanische apparatuur, "inloopstoringen" ondervindt wanneer deze nieuw of recentelijk opnieuw zijn opgebouwd. Als zodanig is het risico op falen het grootst net na de eerste keer opstarten.

Zodra het systeem zijn inloopperiode heeft doorlopen, wat minuten, uren, dagen, weken, maanden of jaren kan duren, afhankelijk van het systeemtype, komt het systeem in een ander risicopatroon. In dit voorbeeld gaat het systeem een ​​periode in waarin het risico op falen toeneemt als functie van de tijd zodra het systeem de inloopperiode verlaat.

De multi-bèta biedt de betrouwbaarheidsingenieur een nauwkeurigere inschatting van het risico als functie van de tijd. Gewapend met deze kennis is hij of zij beter in staat om mitigerende maatregelen te nemen. Tijdens de vroege levensfase zouden we bijvoorbeeld geneigd zijn om de precisie waarmee we produceren/verbouwen, installeren en opstarten te verbeteren. Bovendien kunnen we monitoringtechnieken toevoegen en/of onze monitoringfrequentie verhogen tijdens de periode met hoog risico. Na de inloopperiode kunnen we bewakingstechnieken introduceren die zijn gericht op de tijdafhankelijke slijtagestoringen waarvan wordt aangenomen dat ze het systeem beïnvloeden, de bewakingsfrequentie dienovereenkomstig verhogen of in sommige gevallen 'harde' preventieve onderhoudsacties plannen.

De betrouwbaarheid van het systeem inschatten

Nadat de betrouwbaarheid van componenten of machines is vastgesteld ten opzichte van de bedrijfscontext en de vereiste missietijd, moeten fabrieksingenieurs de betrouwbaarheid van een systeem of proces beoordelen. Nogmaals, omwille van de beknoptheid en eenvoud bespreken we de schattingen van de systeembetrouwbaarheid voor series, parallelle en shared-load redundante systemen (r/n-systemen).

Seriesystemen
Alvorens seriesystemen te bespreken, moeten we betrouwbaarheidsblokdiagrammen bespreken. Geen ingewikkeld hulpmiddel om te gebruiken, betrouwbaarheidsblokdiagrammen brengen eenvoudig een proces van begin tot eind in kaart. Voor een seriesysteem wordt subsysteem A gevolgd door subsysteem B, enzovoort. In het seriesysteem hangt de mogelijkheid om subsysteem B te gebruiken af ​​van de bedrijfsstatus van subsysteem A. Als subsysteem A niet werkt, is het systeem uit, ongeacht de toestand van subsysteem B (Figuur 9).

To calculate the system reliability for a serial process, you only need to multiply the estimated reliability of Subsystem A at time (t) by the estimated reliability of Subsystem B at time (t). The basic equation for calculating the system reliability of a simple series system is:

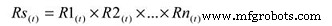
Where:
Rs(t) – System reliability for given time (t)
R1-n(t) – Subsystem or sub-function reliability for given time (t)

So, for a simple system with three subsystems, or sub-functions, each having an estimated reliability of 0.90 (90%) at time (t), the system reliability is calculated as 0.90 X 0.90 X 0.90 =0.729, or about 73%.

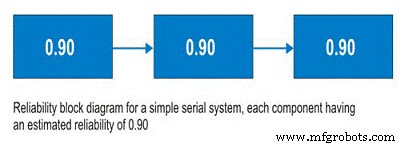
Figure 9. Simple Serial System

Parallel Systems
Often, design engineers will incorporate redundancy into critical machines. Reliability engineers call these parallel systems. These systems may be designed as active parallel systems or standby parallel systems. The block diagram for a simple two component parallel system is shown in Figure 10.

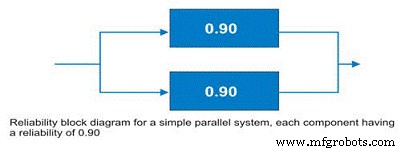
Figure 10. Simple parallel system – the system reliability is increased to 99% due to the redundancy.

To calculate the reliability of an active parallel system, where both machines are running, use the following simple equation:

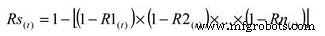
Where:
Rs(t) – System reliability for given time (t)
R1-n(t) – Subsystem or sub-function reliability for given time (t)

The simple parallel system in our example with two components in parallel, each having a reliability of 0.90, has a total system reliability of 1 – (0.1 X 0.1) =0.99. So, the system reliability was significantly improved.

There are some shortcut methods for calculating parallel system reliability when all subsystems have the same estimated reliability. More often, systems contain parallel and serial subcomponents as depicted in Figure 11. The calculation of standby systems requires knowledge about the reliability of the switching mechanism. In the interest of simplicity and brevity, this topic will be reserved for a future article.

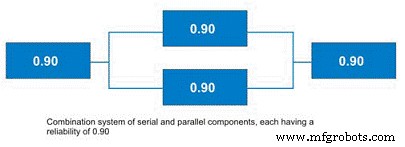
Figure 11. Combination System with Parallel and Serial Elements

r out of n Systems (r/n Systems)
An important concept to plant reliability engineers is the concept of r/n systems. These systems require that r units from a total population in n be available for use. A great industrial example is coal pulverizers in an electric power generating plant. Often, the engineers design this function in the plant using an r/n approach. For instance, a unit has four pulverizers and the unit requires that three of the four be operable to run at the unit’s full load (see Figure 12).

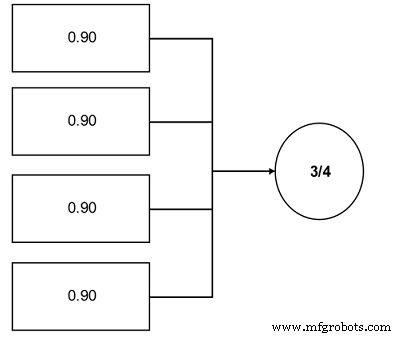
Figure 12. Simple r/n system example – Three of the four components are required.

The reliability calculation for an r/n system can be reduced to a simple cumulative binomial distribution calculation, the formula for which is:

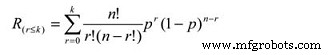
Where:
Rs =System reliability given the actual number of failures (r) is less than or equal the maximum allowable (k)
r =The actual number of failures
k =The maximum allowable number of failures
n =The total number of units in the system
p =The probability of survival, or the subcomponent reliability for a given time (t).

This equation is somewhat more complicated. In our pulverizer example, assuming a subcomponent reliability of 0.90, the equation works out as a summation of the following:
P(0) =0.6561
P(1) =0.2916

So, the likelihood of completing the mission time (t) is 0.9477 (0.6561 + 0.2916), or approximately 95%.

Field Data Collection
To employ the reliability analysis methods described herein, the engineer requires data. It is imperative to establish field data collection systems to support your reliability management initiatives. Likewise, as much as possible, you’ll want to employ common nomenclature and units so that your data can be parsed effectively for more detailed analysis. Collect the following information:

• Basic System Information
• Operating Context
• Environmental Context
• Failure Data

A good general system for data collection is described in the IEC standard 300-3-2. In addition to providing instructions for collecting field data, it provides a standard taxonomy of failure modes. Other taxonomies have been established, but the IEC standard represents a good starting point for your organization to define its own. Likewise, DOE standard NE-1004-92 offers a very nice standard nomenclature of failure causes.

An important benefit derived from your efforts to collect good field data is that it enables you to break the “random trap.” As I mentioned earlier, the bathtub curve has been much maligned – particularly in the Reliability-Centered Maintenance literature. While it’s true that Weibull analysis reveals that few complex mechanical systems exhibit time-dependent wearout failures, the reason, at least in part, is due to the fact that the reliability of complex systems is affected by a wide variety of failure modes and mechanisms.

When these are lumped together, there is a “randomizing” effect, which makes the failures appear to lack any time dependency. However, if the failure modes were analyzed individually, the story would likely be very different (Figure 13). For certain, some failure modes would still be mathematically random, but many, and arguably most, would exhibit a time dependency. This kind of information would arm reliability engineers and managers with a powerful set of options for mitigating failure risk with a high degree of precision. Naturally, this ability depends upon the effective collection and subsequent analysis of field data.

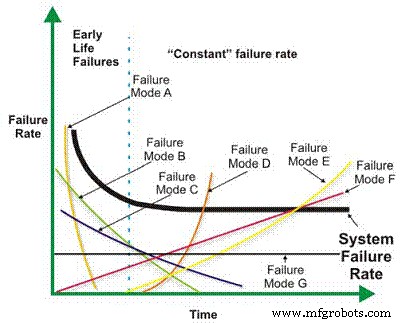
Figure 13. Good field data collection enables you to break the random trap.

This brief introduction to reliability engineering methods is intended to expose the otherwise uninitiated plant engineer to the world of quantitative reliability engineering. The subject is quite broad, however, and I’ve only touched on the major reliability methods that I believe are most applicable to the plant engineer. I encourage you to further investigate the field of reliability engineering methods, concentrating on the following topics, among others:

• More detailed understanding of the Weibull distribution and its applications

• More detailed understanding of the exponential distribution and its applications

• The Gaussian distribution and its applications

• The log-normal distribution and its applications

• Confidence intervals (binomial, chi-square/Poisson, etc.)

• Beta distribution and its applications

• Bayesian applications of reliability engineering methods

• Stress-strength interference analysis

• Testing options and their applicability to plant reliability engineering

• Reliability growth strategies and management

• More detailed understanding of field data collection.

Most important, spend time learning how to apply reliability engineering methods to plant reliability problems. If your interest in reliability engineering methods is high, I encourage you to pursue professional certification by the American Society for Quality as a reliability engineer (CRE).

References
Troyer, D. (2006) Strategic Plant Reliability Management Course Book, Noria Publishing, Tulsa, Oklahoma.

Bernowski, K (1997) “Safety in the Skies,” Quality Progress , January.

Dovich, R. (1990) Reliability Statistics, ASQ Quality Press, Milwaukee, WI.

Krishnamoorthi, K.S. (1992) Reliability Methods for Engineers, ASQ Quality Press , Milwaukee, WI.

MIL Standard 721

IEC Standard 300-3-3

DOE Standard NE-1004-92

Appendix:Select reliability engineering terms from MIL STD 721
Availability – A measure of the degree to which an item is in the operable and committable state at the start of the mission, when the mission is called for at an unknown state.

Capability – A measure of the ability of an item to achieve mission objectives given the conditions during the mission.

Dependability – A measure of the degree to which an item is operable and capable of performing its required function at any (random) time during a specified mission profile, given the availability at the start of the mission.

Failure – The event, or inoperable state, in which an item, or part of an item, does not, or would not, perform as previously specified.

Failure, dependent – Failure which is caused by the failure of an associated item(s). Not independent.

Failure, independent – Failure which occurs without being caused by the failure of any other item. Not dependent.

Failure mechanism – The physical, chemical, electrical, thermal or other process which results in failure.

Failure mode – The consequence of the mechanism through which the failure occurs, i.e. short, open, fracture, excessive wear.

Failure, random – Failure whose occurrence is predictable only in the probabilistic or statistical sense. This applies to all distributions.

Failure rate – The total number of failures within an item population, divided by the total number of life units expended by that population, during a particular measurement interval under stated conditions.

Maintainability – The measure of the ability of an item to be retained or restored to specified condition when maintenance is performed by personnel having specified skill levels, using prescribed procedures and resources, at each prescribed level of maintenance and repair.

Maintenance, corrective – All actions performed, as a result of failure, to restore an item to a specified condition. Corrective maintenance can include any or all of the following steps:localization, isolation, disassembly, interchange, reassembly, alignment and checkout.

Maintenance, preventive – All actions performed in an attempt to retain an item in a specified condition by providing systematic inspection, detection and prevention of incipient failures.

Mean time between failure (MTBF) – A basic measure of reliability for repairable items:the mean number of life units during which all parts of the item perform within their specified limits, during a particular measurement interval under stated conditions.

Mean time to failure (MTTF) – A basic measure of reliability for non-repairable items:The mean number of life units during which all parts of the item perform within their specified limits, during a particular measurement interval under stated conditions.

Mean time to repair (MTTR) – A basic measure of maintainability:the sum of corrective maintenance times at any specified level of repair, divided by the total number of failures within an item repaired at that level, during a particular interval under stated conditions.

Mission reliability – The ability of an item to perform its required functions for the duration of specified mission profile.

Reliability – (1) The duration or probability of failure-free performance under stated conditions. (2) The probability that an item can perform its intended function for a specified interval under stated conditions. For non-redundant items this is the equivalent to definition (1). For redundant items, this is the definition of mission reliability.