Computationele circuits

Wanneer iemand het woord 'computer' noemt, komt meestal een digitaal apparaat in je op. Digitale circuits vertegenwoordigen numerieke grootheden in binair formaat:patronen van enen en nullen vertegenwoordigd door een groot aantal transistorcircuits die in verzadigde of afgesneden toestanden werken. Analoge schakelingen kunnen echter ook worden gebruikt om numerieke grootheden weer te geven en wiskundige berekeningen uit te voeren, door variabele spanningssignalen te gebruiken in plaats van discrete aan/uit-statussen.

Hier is een eenvoudig voorbeeld van binaire (digitale) weergave versus analoge weergave van het getal "vijfentwintig:"

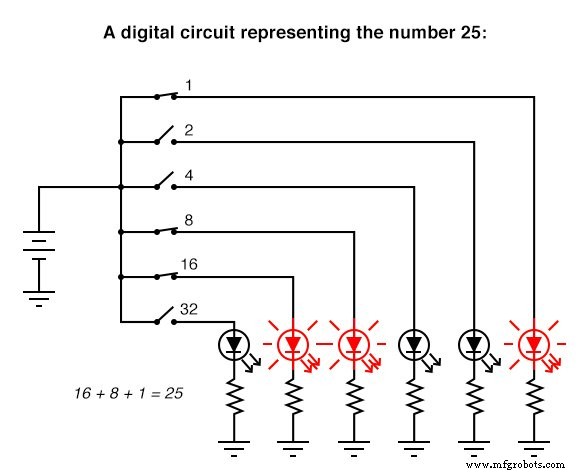
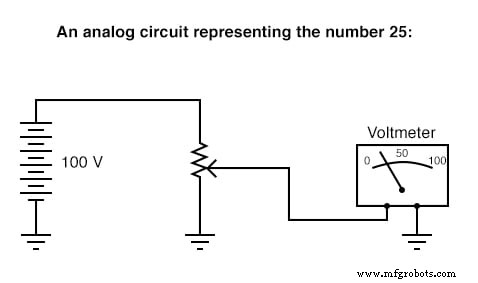
Digitale circuits zijn heel anders dan circuits die op analoge principes zijn gebouwd. Digitale rekencircuits kunnen ongelooflijk complex zijn en berekeningen moeten vaak in opeenvolgende "stappen" worden uitgevoerd om een ​​definitief antwoord te krijgen, net zoals een mens rekenkundige berekeningen in stappen zou uitvoeren met potlood en papier. Analoge rekencircuits zijn daarentegen vrij eenvoudig in vergelijking en voeren hun berekeningen continu en in realtime uit. Er is echter een nadeel aan het gebruik van analoge circuits om getallen weer te geven:onnauwkeurigheid. Het hierboven getoonde digitale circuit vertegenwoordigt precies het getal vijfentwintig. Het hierboven getoonde analoge circuit kan al dan niet exact zijn gekalibreerd op 25.000 volt, maar is onderhevig aan "drift" en fouten.

In toepassingen waar precisie niet van cruciaal belang is, zijn analoge rekencircuits erg praktisch en elegant. Hier worden een paar op-amp-circuits weergegeven voor het uitvoeren van analoge berekeningen:

Computationele op-amp-circuits

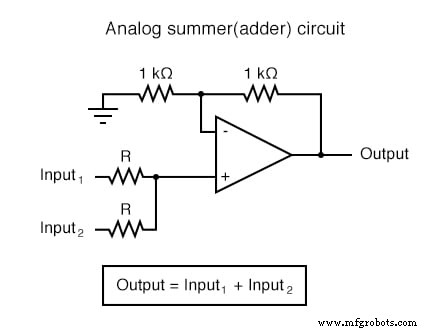
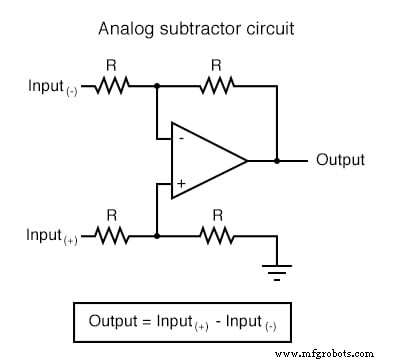
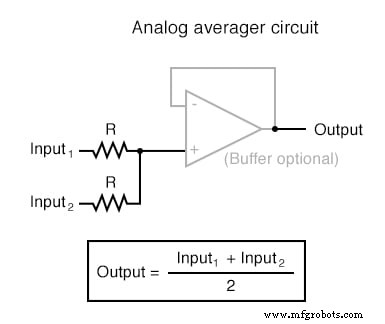
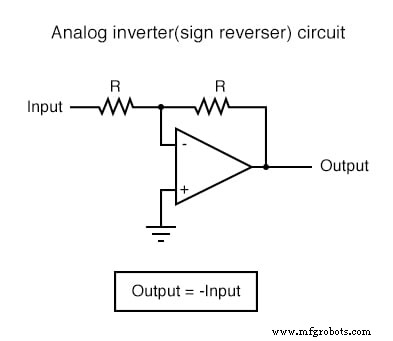
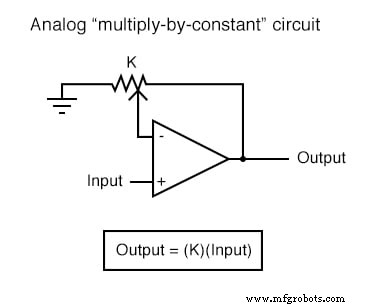
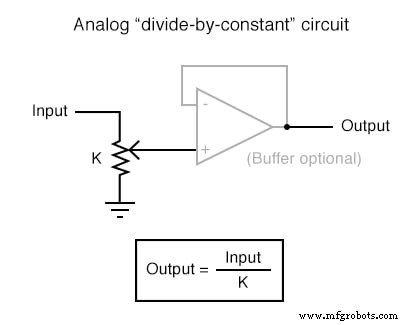
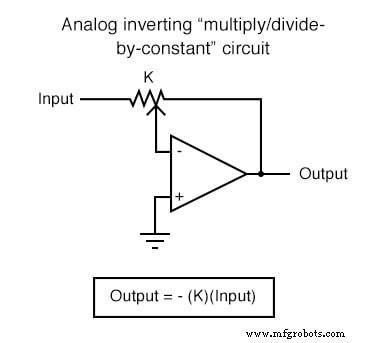
Elk van deze circuits kan op modulaire wijze worden gebruikt om een ​​circuit te creëren dat in staat is tot meerdere berekeningen. Stel bijvoorbeeld dat we een bepaalde fractie van een variabele van een andere variabele moeten aftrekken. Door een deel-door-constante-schakeling te combineren met een aftrekschakeling, konden we de vereiste functie verkrijgen:

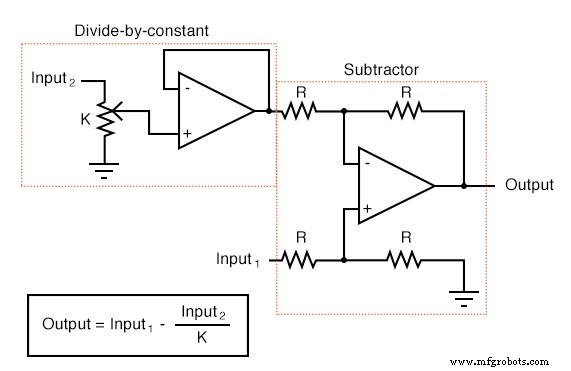
Apparaten genaamd analoge computers was gebruikelijk in universiteiten en technische winkels, waar tientallen op-amp-circuits konden worden "gepatcht" samen met verwijderbare jumperdraden om wiskundige uitspraken te modelleren, meestal met het doel een fysiek proces te simuleren waarvan de onderliggende vergelijkingen bekend waren. Digitale computers hebben analoge computers zo goed als achterhaald gemaakt, maar analoge rekencircuits kunnen niet worden overtroffen door digitaal in termen van pure elegantie en zuinigheid van noodzakelijke componenten.

Analoge rekenschakelingen blinken uit in het uitvoeren van de rekenbewerkingen integratie en differentiatie met betrekking tot tijd, door condensatoren te gebruiken in een op-amp feedbacklus. Om de werking en toepassingen van deze circuits volledig te begrijpen, moeten we echter eerst de betekenis van deze fundamentele calculusconcepten begrijpen. Gelukkig is de toepassing van op-amp-circuits op problemen in de echte wereld met calculus een uitstekend middel om elementaire calculus te onderwijzen. In de woorden van John I. Smith, ontleend aan zijn uitstekende leerboek, Modern Operational Circuit Design :

"Bepaalde lezers worden aangemoedigd:integraalrekening is een van de wiskundige disciplines die operationele [versterker] circuits exploiteren en, in het proces, eerder slopen als een barrière voor begrip." (pag. 4)

De mening van de heer Smith over de pedagogische waarde van analoge schakelingen als leermiddel voor wiskunde zijn niet uniek. Overweeg de mening van ingenieur George Fox Lang, in een artikel dat hij schreef voor het augustus 2000 nummer van het tijdschrift Sound and Vibration , getiteld:"Analoog was niet een computerhandelsmerk!”:

“Het creëren van een echte fysieke entiteit (een circuit) die wordt bestuurd door een bepaalde reeks vergelijkingen en ermee in wisselwerking staat, geeft een uniek inzicht in die wiskundige uitspraken. Er is geen betere manier om een ​​'onderbuikgevoel' te ontwikkelen voor de wisselwerking tussen natuurkunde en wiskunde dan door zo'n interactie te ervaren. De analoge computer was een krachtig interdisciplinair leermiddel; de veroudering ervan wordt betreurd door veel opvoeders op verschillende gebieden.” (pag. 23)

Differentiatie is de eerste bewerking die typisch wordt geleerd door beginnende calculusstudenten. Simpel gezegd, differentiatie is het bepalen van de momentane veranderingssnelheid van een variabele in relatie tot een andere. In analoge differentiatorcircuits is de onafhankelijke variabele tijd, en dus zijn de veranderingssnelheden waarmee we te maken hebben de veranderingssnelheden voor een elektronisch signaal (spanning of stroom) met betrekking tot tijd.

Stel dat we de positie van een auto zouden meten, rijdend in een direct pad (geen bochten), vanaf het startpunt. Laten we deze meting x . noemen . Als de auto met een zodanige snelheid beweegt dat de afstand vanaf "start" in de loop van de tijd gestaag toeneemt, wordt zijn positie in een grafiek weergegeven als een lineaire functie (rechte lijn):

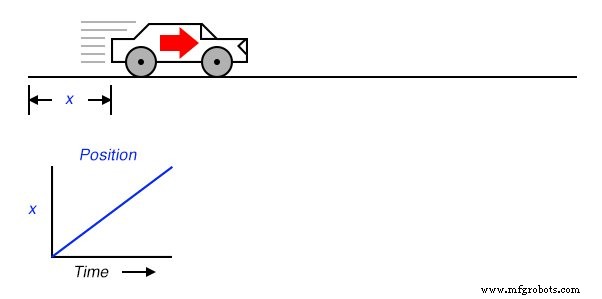
Als we de afgeleide . zouden berekenen van de positie van de auto met betrekking tot de tijd (dat wil zeggen, het bepalen van de veranderingssnelheid van de positie van de auto met betrekking tot de tijd), zouden we komen tot een grootheid die de snelheid van de auto vertegenwoordigt. De differentiatiefunctie wordt weergegeven door de fractionele notatie d/d , dus bij het differentiëren van positie (x ) met betrekking tot tijd (t ), geven we het resultaat (de afgeleide) aan als dx/dt :

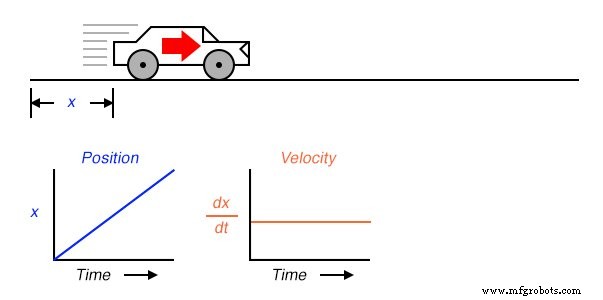
Voor een lineaire grafiek van x na verloop van tijd, de afgeleide van positie (dx/dt ), anders en beter bekend als velocity , zal een vlakke lijn zijn, onveranderlijk in waarde. De afgeleide van een wiskundige functie kan grafisch worden opgevat als zijn helling wanneer uitgezet in een grafiek, en hier kunnen we zien dat de positie (x ) grafiek heeft een constante helling, wat betekent dat zijn afgeleide (dx/dt ) moet constant zijn in de tijd.

Stel nu dat de afstand die de auto aflegde in de loop van de tijd exponentieel toenam:dat wil zeggen, hij begon zijn reis in langzame bewegingen, maar legde meer extra afstand af met elke voorbijgaande periode in de tijd. We zouden dan zien dat de afgeleide van positie (dx/dt ), ook wel bekend als snelheid (v ), zou niet constant zijn in de tijd, maar zou toenemen:

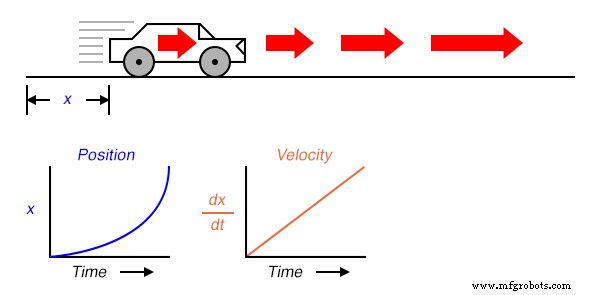
De hoogte van punten op de snelheidsgrafiek komt overeen met de veranderingssnelheden, of helling, van punten op overeenkomstige tijden in de positiegrafiek:

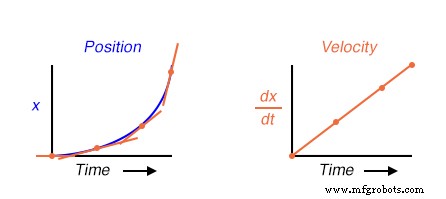
Wat heeft dit te maken met analoge elektronische schakelingen? Welnu, als we een analoog spanningssignaal zouden hebben dat de positie van de auto vertegenwoordigt (denk aan een enorme potentiometer waarvan de wisser aan de auto was bevestigd, waardoor een spanning wordt gegenereerd die evenredig is aan de positie van de auto), zouden we een differentiatorcircuit op dit signaal kunnen aansluiten en hebben het circuit berekent continu de snelheid van de auto, waarbij het resultaat wordt weergegeven via een voltmeter die is aangesloten op de uitgang van het differentiatorcircuit:

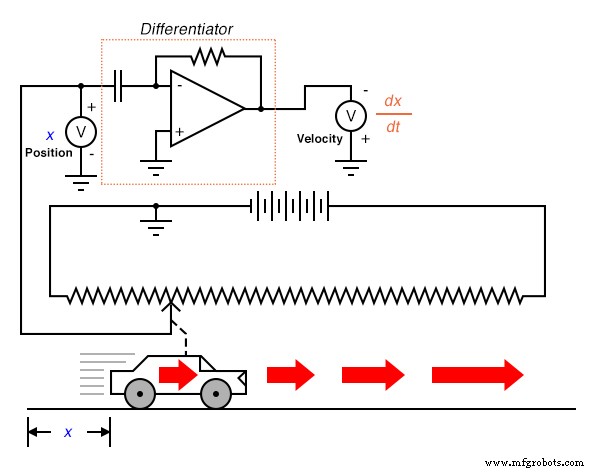
Bedenk uit het vorige hoofdstuk dat een differentiatorschakeling een spanning afgeeft die evenredig is met de veranderingssnelheid van de ingangsspanning in de tijd (d/dt ). Dus als de ingangsspanning in de loop van de tijd verandert met een constante snelheid , zal de uitgangsspanning een constante waarde hebben. Als de auto zo beweegt dat de afgelegde afstand in de loop van de tijd met een constante snelheid toeneemt, betekent dit dat de auto met een constante snelheid rijdt, en het differentiatorcircuit zal een constante spanning afgeven die evenredig is met die snelheid. Als de afgelegde afstand van de auto in de loop van de tijd op een niet-stabiele manier verandert, zal de output van het differentiatorcircuit eveneens niet-stabiel zijn, maar altijd op een niveau dat representatief is voor de veranderingssnelheid van de input in de tijd.

Merk op dat de voltmeter die de snelheid registreert (aan de uitgang van het differentiatorcircuit) in "omgekeerde" polariteit is aangesloten op de uitgang van de op-amp. Dit komt omdat het getoonde differentiatorcircuit inverterend is :het uitvoeren van een negatieve spanning voor een positieve veranderingssnelheid van de ingangsspanning. Als we willen dat de voltmeter een positieve waarde voor snelheid registreert, moet deze worden aangesloten op de op-amp zoals weergegeven. Hoe onpraktisch het ook mag zijn om een ​​gigantische potentiometer aan te sluiten op een bewegend object zoals een auto, het concept moet duidelijk zijn:door elektronisch de calculusfunctie van differentiatie uit te voeren op een signaal dat de positie vertegenwoordigt, verkrijgen we een signaal dat de snelheid vertegenwoordigt.

Beginnende calculusstudenten leren symbolische technieken voor differentiatie. Dit vereist echter dat de vergelijking die de oorspronkelijke grafiek beschrijft bekend is. Zo leren calculusstudenten hoe ze een functie kunnen aannemen zoals y =3x en vind zijn afgeleide met betrekking tot x (d/dx ), 3 , simpelweg door de vergelijking te manipuleren. We kunnen de nauwkeurigheid van deze manipulatie verifiëren door de grafieken van de twee functies te vergelijken:

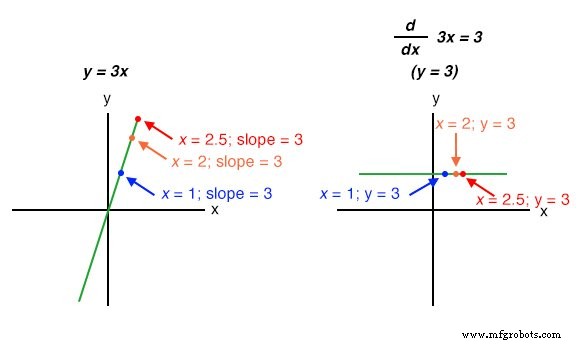
Niet-lineaire functies zoals y =3x ² kan ook worden onderscheiden door symbolische middelen. In dit geval is de afgeleide van y =3x ² met betrekking tot x is 6x :

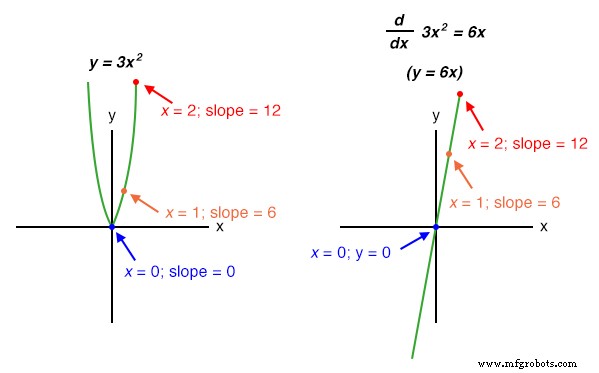
In het echte leven kunnen we het gedrag van een fysieke gebeurtenis echter vaak niet beschrijven met een simpele vergelijking zoals y =3x , en dus kan symbolische differentiatie van het type dat door calculusstudenten wordt geleerd, onmogelijk zijn om toe te passen op een fysieke meting. Als iemand de afgeleide van de positie van onze hypothetische auto (dx/dt =snelheid) met symbolische middelen, zouden ze eerst een vergelijking moeten krijgen die de positie van de auto in de tijd beschrijft, gebaseerd op positiemetingen uit een echt experiment - een bijna onmogelijke taak tenzij de auto wordt bestuurd onder zorgvuldig gecontroleerde omstandigheden, wat leidt tot een zeer eenvoudige positie grafiek. Echter, een analoge differentiatorschakeling, door gebruik te maken van het gedrag van een condensator met betrekking tot spanning, stroom en tijd i =C(dv/dt) , onderscheidt natuurlijk elk echt signaal in relatie tot tijd, en zou een signaal kunnen uitvoeren dat overeenkomt met de momentane snelheid (dx/dt ) op elk moment. Door het positiesignaal van de auto samen met het uitgangssignaal van de differentiator te loggen met behulp van een kaartrecorder of ander data-acquisitieapparaat, zouden beide grafieken zichzelf natuurlijk presenteren voor inspectie en analyse.

We kunnen het principe van differentiatie nog een stap verder brengen door het toe te passen op het snelheidssignaal met behulp van een ander differentiatorcircuit. Met andere woorden, gebruik het om de veranderingssnelheid van de snelheid te berekenen, waarvan we weten dat het de veranderingssnelheid van de positie is. Tot welke praktische maatregel zouden we komen als we dit zouden doen? Denk hierbij aan de eenheden die we gebruiken om positie en snelheid te meten. Als we de positie van de auto vanaf het beginpunt in mijlen zouden meten, dan zouden we de snelheid waarschijnlijk uitdrukken in eenheden van mijlen per uur (dx/dt ). Als we de snelheid (gemeten in mijl per uur) zouden differentiëren met de tijd, zouden we eindigen met een eenheid van mijl per uur per uur . Inleidende natuurkundelessen leren studenten over het gedrag van vallende voorwerpen, het meten van positie in meters , snelheid in meters per seconde , en verandering in snelheid in de loop van de tijd in meters per seconde, per seconde . Deze laatste maat heet versnelling :de snelheid waarmee de snelheid in de loop van de tijd verandert:

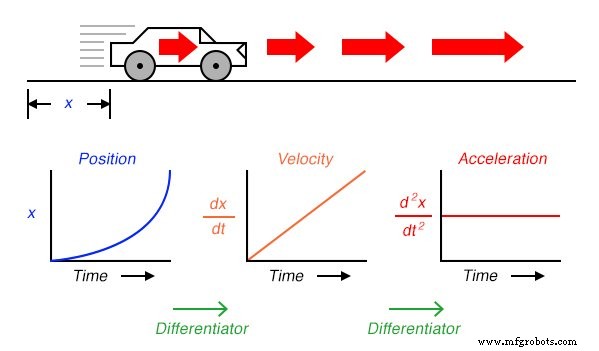
De uitdrukking d ² x/dt ² heet de tweede afgeleide van positie (x ) met betrekking tot tijd (t ). Als we een tweede differentiatorcircuit zouden aansluiten op de uitgang van de eerste, zou de laatste voltmeter versnelling registreren:

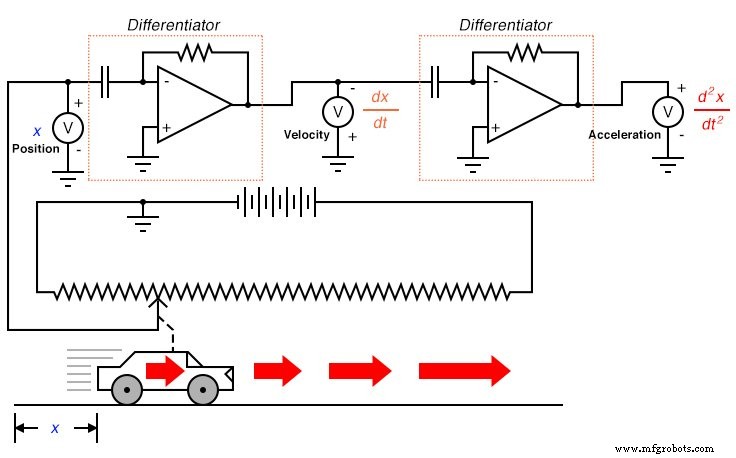
Door snelheid af te leiden uit positie en versnelling uit snelheid, zien we het principe van differentiatie heel duidelijk geïllustreerd. Dit zijn niet de enige fysieke metingen die op deze manier aan elkaar gerelateerd zijn, maar ze zijn misschien wel de meest voorkomende. Een ander voorbeeld van calculus in actie is de relatie tussen vloeistofstroom (q ) en vloeistofvolume (v ) die zich in de loop van de tijd in een vat hebben opgehoopt:

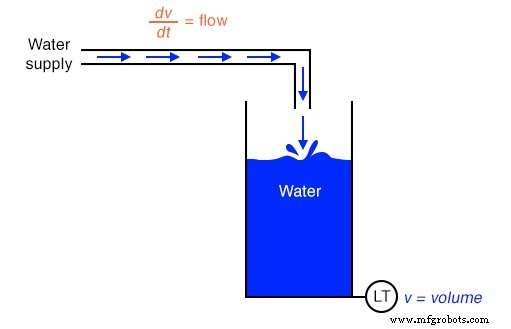
Een "niveauzender"-apparaat dat op een wateropslagtank is gemonteerd, geeft een signaal dat recht evenredig is met het waterniveau in de tank, wat - als de tank een constant dwarsdoorsnede-oppervlak heeft over de hele hoogte - direct gelijk is aan het opgeslagen watervolume. Als we dit volumesignaal zouden nemen en het differentiëren met betrekking tot tijd (dv/dt ), zouden we een signaal verkrijgen dat evenredig is met de stroomsnelheid van het water door de leiding die water naar de tank voert. Een differentiatorcircuit dat zo is aangesloten dat dit volumesignaal wordt ontvangen, zou een uitgangssignaal produceren dat evenredig is met de stroom, mogelijk in de plaats van een stroommeetapparaat ("Flow Transmitter") dat in de leiding is geïnstalleerd.

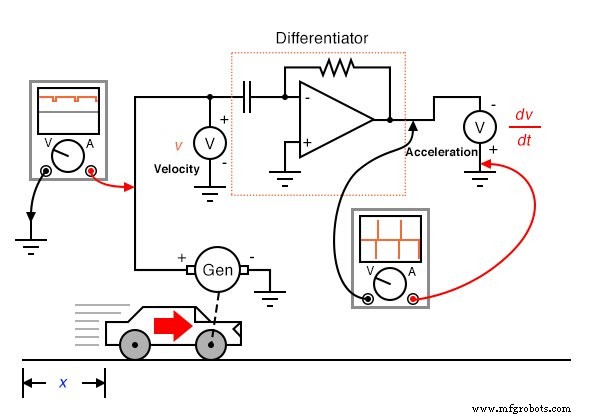
Terugkerend naar het auto-experiment, veronderstel dat onze hypothetische auto was uitgerust met een tachogenerator op een van de wielen, die een spanningssignaal produceert dat recht evenredig is met de snelheid. We kunnen het signaal differentiëren om versnelling te verkrijgen met één circuit, zoals dit:

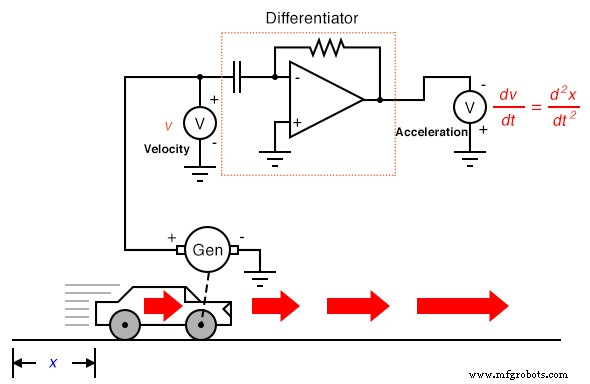
Door zijn aard differentieert de tachogenerator de positie van de auto met betrekking tot de tijd en genereert hij een spanning die evenredig is met hoe snel de hoekpositie van het wiel in de loop van de tijd verandert. Dit geeft ons een onbewerkt signaal dat al representatief is voor de snelheid, met slechts een enkele differentiatiestap die nodig is om een ​​versnellingssignaal te verkrijgen. Een tachogenerator die de snelheid meet, is natuurlijk een veel praktischer voorbeeld van auto-instrumentatie dan een gigantische potentiometer die zijn fysieke positie meet, maar wat we praktisch winnen, verliezen we bij positiemeting. Hoe vaak we ook differentiëren, we kunnen de positie van de auto nooit afleiden uit een snelheidssignaal. Als het differentiatieproces ons van positie naar snelheid naar versnelling bracht, dan moeten we op de een of andere manier het "omgekeerde" differentiatieproces uitvoeren om van snelheid naar positie te gaan. Zo'n wiskundig proces bestaat, en het heet integratie . De "integrator"-schakeling kan worden gebruikt om deze functie van integratie met betrekking tot tijd uit te voeren:

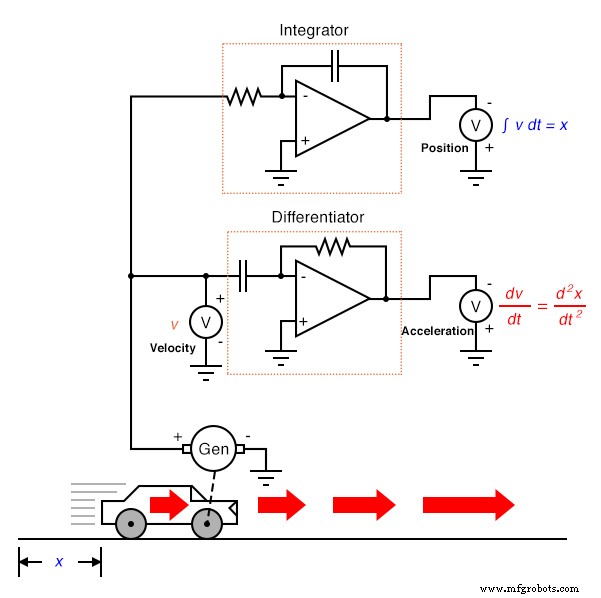
Bedenk uit het vorige hoofdstuk dat een integratorschakeling een spanning afgeeft waarvan de veranderingssnelheid in de tijd evenredig is met de grootte van de ingangsspanning. Dus, gegeven een constante ingangsspanning, zal de uitgangsspanning veranderen met een constante snelheid . Als de auto met een constante snelheid rijdt (constante ingangsspanning naar het integratorcircuit van de tachogenerator), dan zal de afgelegde afstand gestaag toenemen naarmate de tijd vordert, en de integrator zal een gestaag veranderende spanning afgeven die evenredig is met die afstand. Als de snelheid van de auto niet constant is, zal de veranderingssnelheid in de loop van de tijd ook niet van de uitgang van het integratorcircuit zijn, maar de uitgangsspanning zal een getrouwe weergave van de afstand die de auto op een bepaald moment heeft afgelegd.

Het symbool voor integratie lijkt op een zeer smalle, cursieve letter "S" (∫). De vergelijking die dit symbool gebruikt (∫v dt =x ) vertelt ons dat we snelheid integreren (v ) met betrekking tot tijd (dt ), en het verkrijgen van positie (x ) als resultaat.

We kunnen dus drie maten van de beweging van de auto (positie, snelheid en versnelling) uitdrukken in termen van snelheid (v ) net zo gemakkelijk als we konden in termen van positie (x ):

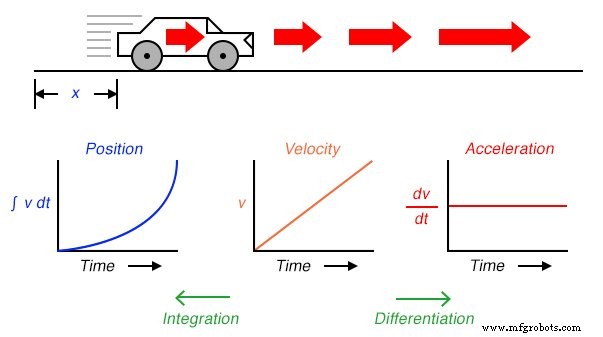
Als we een accelerometer aan de auto hadden bevestigd, die een signaal genereert dat evenredig is met de snelheid van acceleratie of deceleratie, zouden we (hypothetisch) een snelheidssignaal kunnen verkrijgen met één integratiestap, en een positiesignaal met een tweede integratiestap:

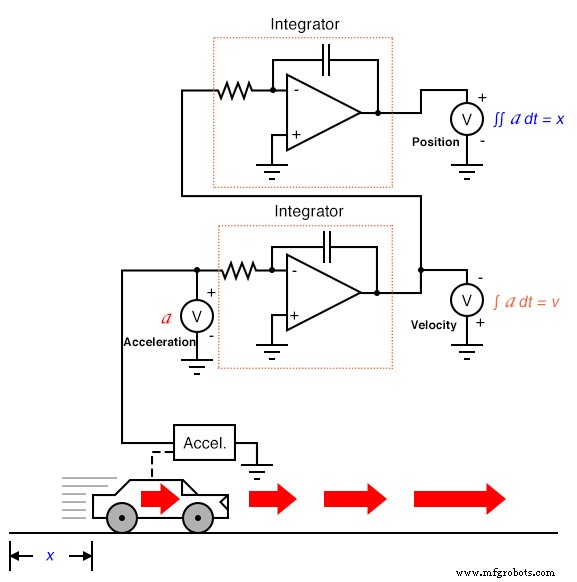
Alle drie de maten van de beweging van de auto (positie, snelheid en versnelling) kunnen dus worden uitgedrukt in termen van versnelling:

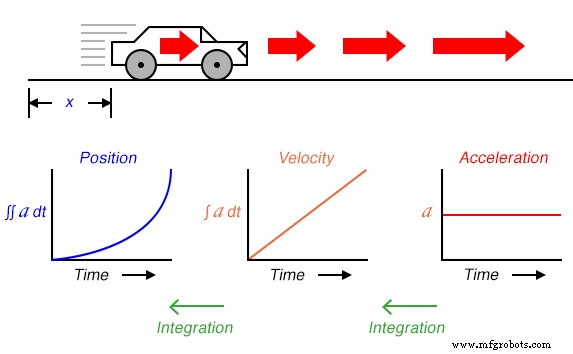
Zoals je misschien al vermoedde, kan het integratieproces ook worden geïllustreerd in en toegepast op andere fysieke systemen. Neem bijvoorbeeld de wateropslagtank en het eerder getoonde stroomvoorbeeld. Als de stroomsnelheid het derivaat is van tankvolume met betrekking tot tijd (q =dv/dt ), dan zouden we ook kunnen zeggen dat volume de integraal . is van stroomsnelheid met betrekking tot tijd:

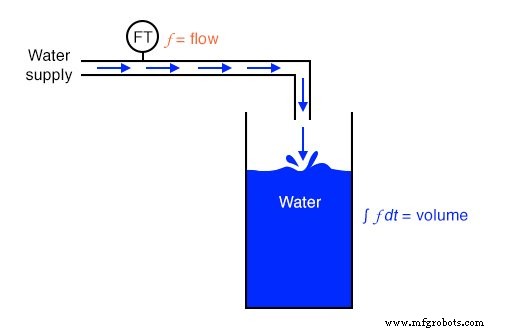
Als we een "Flow Transmitter" -apparaat zouden gebruiken om de waterstroom te meten, dan zouden we door tijdintegratie het volume water kunnen berekenen dat zich in de tank in de loop van de tijd heeft verzameld. Hoewel het theoretisch mogelijk is om een ​​capacitief op-amp-integratorcircuit te gebruiken om een ​​volumesignaal af te leiden van een stromingssignaal, zijn mechanische en digitale elektronische "integrator" -apparaten meer geschikt voor integratie gedurende lange tijdsperioden en worden ze vaak gebruikt in het water behandelings- en distributie-industrieën.

Net zoals er symbolische technieken voor differentiatie zijn, zijn er ook symbolische technieken voor integratie, hoewel ze vaak complexer en gevarieerder zijn. Het toepassen van symbolische integratie op een reëel probleem zoals de versnelling van een auto is echter nog steeds afhankelijk van de beschikbaarheid van een vergelijking die het gemeten signaal nauwkeurig beschrijft - vaak een moeilijk of onmogelijk iets om uit gemeten gegevens af te leiden. Elektronische integratorschakelingen voeren deze wiskundige functie echter continu, in realtime en voor elke . uit ingangssignaalprofiel, waardoor het een krachtig hulpmiddel is voor wetenschappers en ingenieurs.

Dit gezegd hebbende, zijn er kanttekeningen bij het gebruik van calculustechnieken om het ene type meting uit het andere af te leiden. Differentiatie heeft de ongewenste neiging om "ruis" in de gemeten variabele te versterken, aangezien de ruis typisch zal verschijnen als frequenties die veel hoger zijn dan de gemeten variabele, en hoge frequenties hebben van nature een hoge mate van verandering in de tijd.

Stel dat we, om dit probleem te illustreren, een meting van autoversnelling afleiden uit het snelheidssignaal dat wordt verkregen van een tachogenerator met versleten borstels of commutatorstaven. Punten van slecht contact tussen borstel en commutator zullen tijdelijke "dips" in de uitgangsspanning van de tachogenerator produceren, en het differentiatorcircuit dat erop is aangesloten, zal deze dips interpreteren als zeer snelle veranderingen in snelheid. Voor een auto die met constante snelheid rijdt - niet versnellend of vertragend - moet het acceleratiesignaal 0 volt zijn, maar "ruis" in het snelheidssignaal veroorzaakt door een defecte tachogenerator zal ervoor zorgen dat het gedifferentieerde (versnellings)signaal "pieken" bevat, wat ten onrechte aangeeft korte perioden van hoge versnelling en vertraging:

Ruisspanning aanwezig in een te differentiëren signaal hoeft geen significante amplitude te hebben om problemen te veroorzaken:het enige dat nodig is, is dat het ruisprofiel snelle stijg- of daaltijden heeft. Met andere woorden, alle elektrische ruis met een hoge dv/dt component zal problematisch zijn wanneer het wordt gedifferentieerd, zelfs als het een lage amplitude heeft.

Opgemerkt moet worden dat dit probleem geen artefact is (een eigenaardige fout van het meet-/rekeninstrument) van het analoge circuit; het is eerder inherent aan het proces van differentiatie. Het maakt niet uit hoe we de differentiatie uitvoeren, "ruis" in het snelheidssignaal zal onveranderlijk het uitgangssignaal aantasten. Als we een signaal twee keer differentiëren, zoals we deden om zowel snelheid als versnelling uit een positiesignaal te verkrijgen, zal het versterkte ruissignaal dat door het eerste differentiatorcircuit wordt uitgevoerd, opnieuw worden versterkt door de volgende differentiator, waardoor het probleem groter wordt:

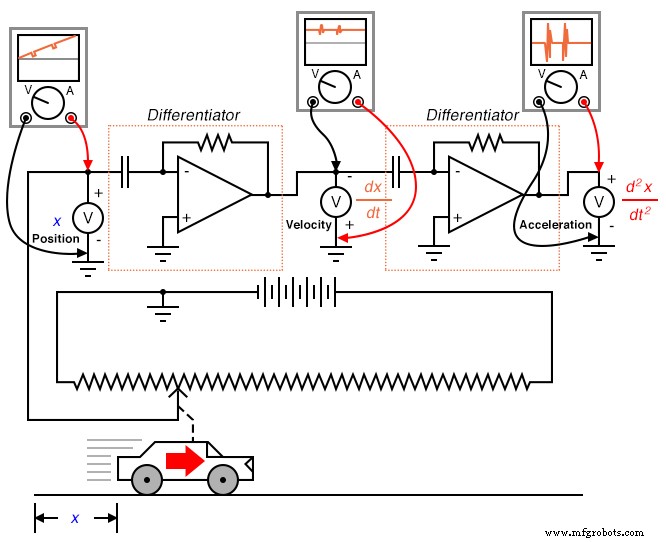
Integratie heeft geen last van dit probleem, omdat integrators fungeren als laagdoorlaatfilters, die hoogfrequente ingangssignalen verzwakken. In feite worden alle hoge en lage pieken die het gevolg zijn van ruis op het signaal in de loop van de tijd gemiddeld, voor een verminderd nettoresultaat. Je zou dus kunnen veronderstellen dat we alle problemen zouden kunnen vermijden door versnelling direct te meten en dat signaal te integreren om snelheid te verkrijgen; in feite, in "omgekeerde" berekening van de manier die eerder is getoond:

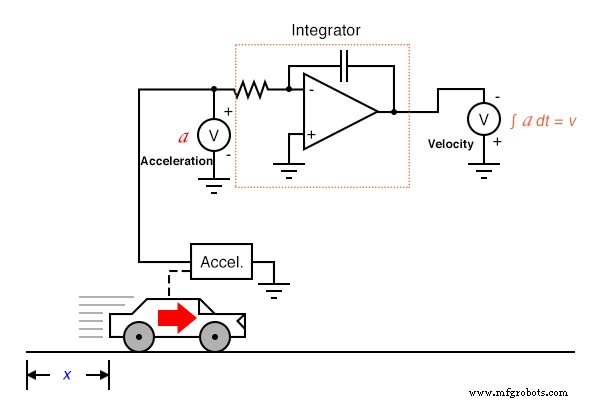
Helaas kan het volgen van deze methodologie ons in andere problemen brengen, waaronder een veel voorkomend artefact van analoge integratorcircuits, bekend als drift . Alle op-amps hebben een bepaalde hoeveelheid ingangsbiasstroom, en deze stroom zal ertoe leiden dat een lading zich ophoopt op de condensator naast de lading die zich ophoopt als gevolg van het ingangsspanningssignaal. Met andere woorden, alle analoge integratorcircuits hebben de neiging dat hun uitgangsspanning "afwijkt" of "kruipt", zelfs als er absoluut geen spanningsingang is, met als gevolg dat de fouten in de loop van de tijd toenemen. Ook zullen imperfecte condensatoren de neiging hebben om hun opgeslagen lading in de loop van de tijd te verliezen als gevolg van interne weerstand, wat resulteert in "drift" naar nul uitgangsspanning. Deze problemen zijn artefacten van de analoge circuits, en kunnen worden geëlimineerd door het gebruik van digitale berekening.

Ondanks circuitartefacten kunnen mogelijke fouten het gevolg zijn van de integratie van één meting (zoals versnelling) om een ​​andere (zoals snelheid) te verkrijgen, simpelweg vanwege de manier waarop integratie werkt. Als het "nul"-kalibratiepunt van de onbewerkte signaalsensor niet perfect is, zal het een licht positief of negatief signaal afgeven, zelfs in omstandigheden waarin het niets zou moeten produceren. Overweeg een auto met een onvolmaakt gekalibreerde versnellingsmeter, of een die wordt beïnvloed door de zwaartekracht om een ​​lichte versnelling te detecteren die niets met de autobeweging te maken heeft. Zelfs met een perfect integrerende computer zal deze sensorfout ervoor zorgen dat de integrator een fout accumuleert, wat resulteert in een uitgangssignaal dat een verandering van snelheid aangeeft wanneer de auto niet versnelt of vertraagt.

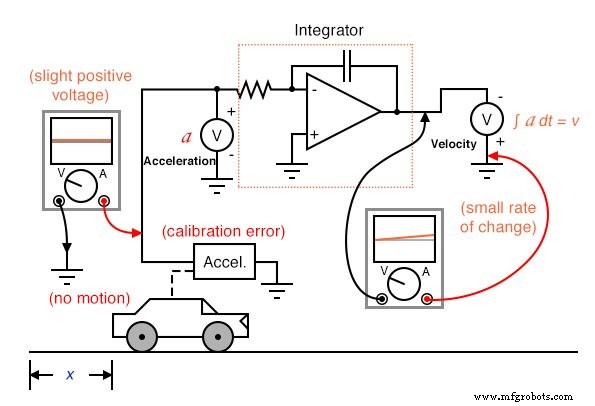
Net als bij differentiatie, wordt deze fout ook groter als het geïntegreerde signaal wordt doorgegeven aan een ander integratorcircuit, omdat de "afdrijvende" uitgang van de eerste integrator zeer binnenkort een significant positief of negatief signaal zal geven voor de volgende integrator om te integreren. Wees daarom voorzichtig bij het integreren van sensorsignalen:als de "nul"-instelling van de sensor niet perfect is , zal het geïntegreerde resultaat afwijken, zelfs als het integratorcircuit zelf perfect is.

Tot nu toe zijn de enige integratiefouten die zijn besproken van kunstmatige aard:afkomstig van onvolkomenheden in de schakelingen en sensoren. Er bestaat ook een bron van fouten die inherent zijn aan het integratieproces zelf, en dat is de onbekende constante probleem. Beginnende calculusstudenten leren dat wanneer een functie wordt geïntegreerd, er een onbekende constante bestaat (meestal weergegeven als de variabele C ) toegevoegd aan het resultaat. Deze onzekerheid is het gemakkelijkst te begrijpen door de afgeleiden van verschillende functies te vergelijken die alleen verschillen door de toevoeging van een constante waarde:

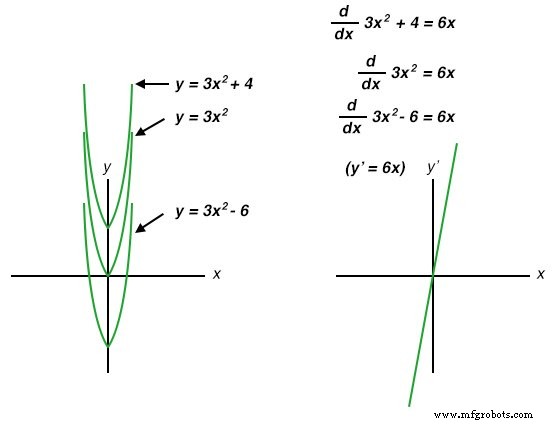
Merk op hoe elk van de parabolische krommen (y =3x ² + C ) delen exact dezelfde vorm, die van elkaar verschillen wat betreft hun verticale offset. Ze delen echter allemaal exact dezelfde afgeleide functie:y’ =(d/dx)( 3x ² + C) =6x , omdat ze allemaal identieke veranderingspercentages delen (hellingen) op overeenkomstige punten langs de x as. Hoewel dit heel natuurlijk lijkt en verwacht wordt vanuit het perspectief van differentiatie (verschillende vergelijkingen delen een gemeenschappelijke afgeleide), komt het beginnende studenten meestal als vreemd over vanuit het perspectief van integratie, omdat er meerdere juiste antwoorden zijn voor de integraal van een functie. Als we van een vergelijking naar zijn afgeleide gaan, is er maar één antwoord, maar als we van die afgeleide teruggaan naar de oorspronkelijke vergelijking, komen we uit bij een reeks correcte oplossingen. Ter ere van deze onzekerheid wordt de symbolische functie van integratie de onbepaalde integraal genoemd .

Wanneer een integrator live signaalintegratie uitvoert met betrekking tot tijd, is de output de som van het geïntegreerde inputsignaal in de tijd en een initiële waarde van willekeurige grootte, die de reeds bestaande output van de integrator vertegenwoordigt op het moment dat de integratie begon. Als ik bijvoorbeeld de snelheid van een auto integreer die in een rechte lijn weg van een stad rijdt, dan zal de berekening dat een constante snelheid van 80 mijl per uur over een tijd van 2 uur een afstand opleveren (∫v dt ) van 100 mijl, betekent dat niet noodzakelijk dat de auto na 2 uur 100 mijl van de stad verwijderd is. Het enige wat het ons vertelt is dat de auto 100 mijl verder zal zijn weg van de stad na 2 uur rijden. De werkelijke afstand vanaf de stad na 2 uur rijden hangt af van hoe ver de auto van de stad was toen de integratie begon. Als we deze initiële waarde voor afstand niet weten, kunnen we de exacte afstand van de auto tot de stad niet bepalen na 2 uur rijden.

Hetzelfde probleem treedt op wanneer we versnelling integreren met betrekking tot tijd om snelheid te verkrijgen:

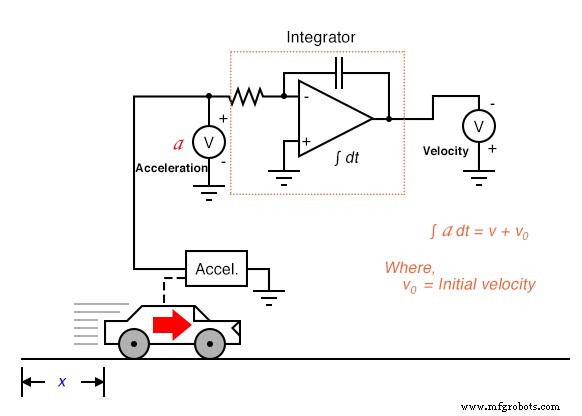
In dit integratorsysteem is de berekende snelheid van de auto alleen geldig als het integratorcircuit is geïnitialiseerd naar een uitgangswaarde van nul wanneer de auto stilstaat (v =0). Anders zou de integrator heel goed een niet-nul signaal kunnen afgeven voor snelheid (v₀ ) wanneer de auto stilstaat, want de accelerometer kan het verschil niet zien tussen een stationaire toestand (0 mijl per uur) en een toestand van constante snelheid (bijvoorbeeld 60 mijl per uur, onveranderlijk). Deze onzekerheid in de output van de integrator is inherent aan het integratieproces en niet een artefact van de schakelingen of van de sensor.

Samengevat, als maximale nauwkeurigheid gewenst is voor een fysieke meting, is het het beste om die variabele direct te meten in plaats van deze uit andere metingen te berekenen. Dit wil niet zeggen dat de berekening waardeloos is. Integendeel, het is vaak het enige praktische middel om een ​​gewenste meting te verkrijgen. De limieten van de berekening moeten echter worden begrepen en gerespecteerd om nauwkeurige metingen te verkrijgen.

GERELATEERD WERKBLAD:

• Werkblad voor lineaire rekenschakelingen