Decibel

De Bel wordt gebruikt om winst weer te geven

In zijn eenvoudigste vorm, de versterking . van een versterker is een verhouding tussen output en input. Zoals alle ratio's is deze vorm van winst unitless. Er is echter een werkelijke eenheid die bedoeld is om winst weer te geven, en deze wordt de bel . genoemd .

Als een eenheid is de bel eigenlijk ontworpen als een handige manier om het verlies van de macht weer te geven in telefoonsysteembedrading in plaats van winst bij versterkers. De naam van het apparaat is afgeleid van Alexander Graham Bell, de beroemde Schotse uitvinder wiens werk een belangrijke rol speelde bij de ontwikkeling van telefoonsystemen. Oorspronkelijk vertegenwoordigde de bel de hoeveelheid signaalvermogensverlies als gevolg van weerstand over een standaardlengte van elektrische kabel. Nu wordt het gedefinieerd in termen van de gemeenschappelijke (grondtal 10) logaritme van een vermogensverhouding (uitgangsvermogen gedeeld door ingangsvermogen):

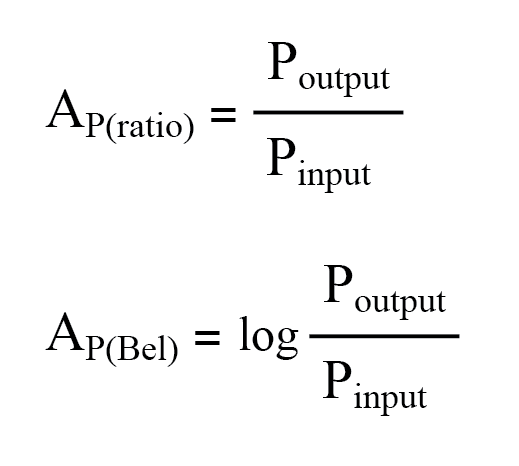
De Bel is niet-lineair

Omdat de bel een logaritmische eenheid is, is deze niet-lineair. Om u een idee te geven van hoe dit werkt, kunt u de volgende tabel met cijfers bekijken, waarin vermogensverliezen en winsten in bels worden vergeleken met eenvoudige verhoudingen:

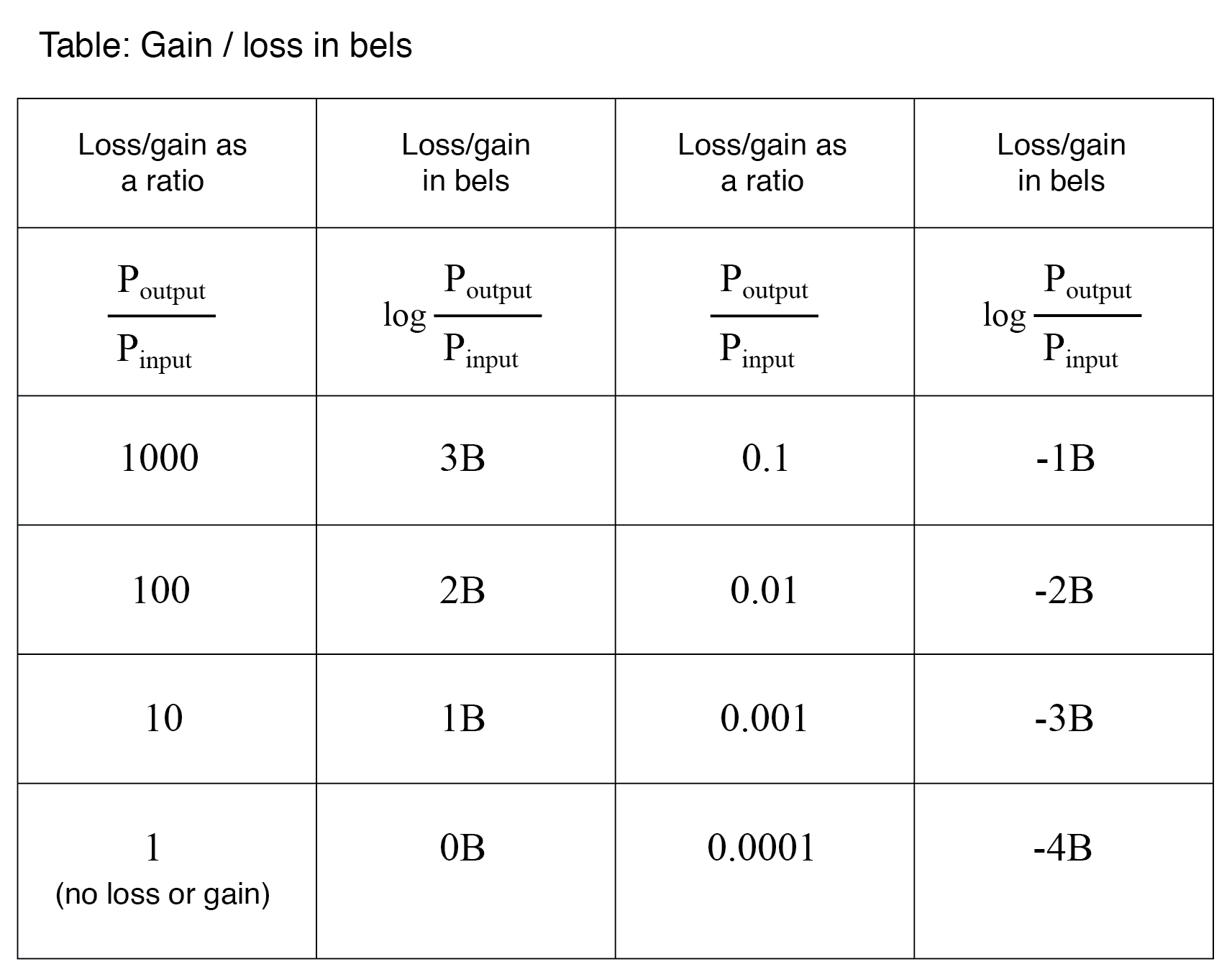
Van de bel naar de decibel gaan

Later werd besloten dat de bel een te grote eenheid was om direct te gebruiken, en daarom werd het gebruikelijk om het metrische voorvoegsel deci toe te passen. (wat 1/10 betekent) ervoor, waardoor het deci . wordt bel of dB. Nu is de uitdrukking "dB" zo gewoon dat veel mensen zich niet realiseren dat het een combinatie is van "deci-" en "-bel", of dat er zelfs zo'n eenheid is als de "bel". Om dit in perspectief te plaatsen, is hier nog een tabel waarin de vermogenswinst/verliesverhoudingen worden vergeleken met decibel:

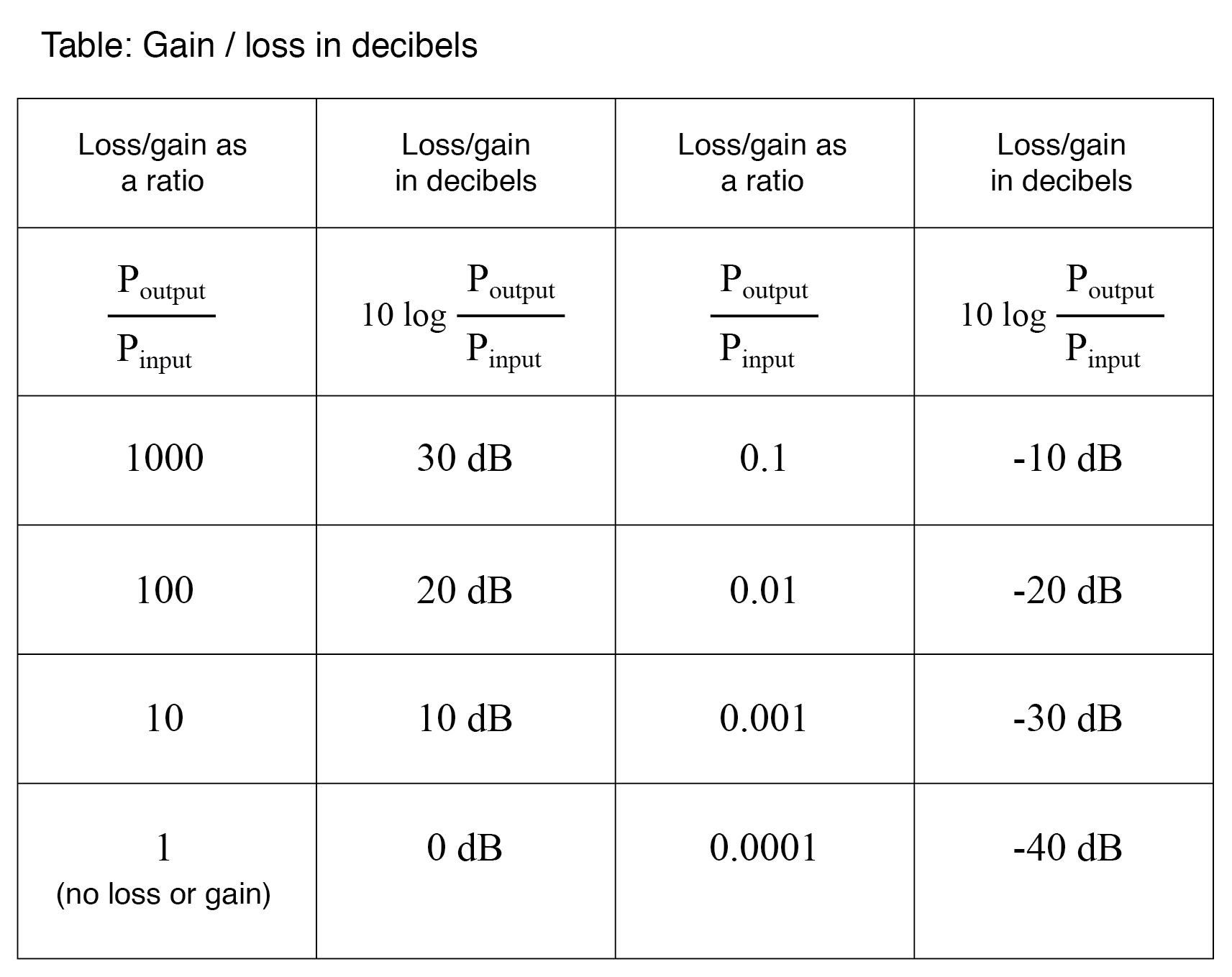
Als logaritmische eenheid bestrijkt deze modus voor het uitdrukken van vermogensversterking een breed scala aan verhoudingen met een minimale spanwijdte in cijfers. Het is redelijk om te vragen, "waarom heeft iemand de behoefte gevoeld om een ​​logaritmische eenheid voor verlies van elektrisch signaal in een telefoonsysteem?” Het antwoord houdt verband met de dynamiek van het menselijk gehoor, waarvan de waarnemingsintensiteit logaritmisch van aard is.

Menselijk gehoor is niet-lineair

Het menselijk gehoor is in hoge mate niet-lineair:om de waargenomen intensiteit van een geluid te verdubbelen, moet het werkelijke geluidsvermogen met een factor tien worden vermenigvuldigd. Het is in deze context volkomen logisch om het vermogensverlies van het telefoonsignaal te relateren aan de logaritmische "bel" -schaal:een vermogensverlies van 1 bel vertaalt zich in een waargenomen geluidsverlies van 50 procent, of 1/2. Een vermogenswinst van 1 bel vertaalt zich in een verdubbeling van de waargenomen intensiteit van het geluid.

Andere voorbeelden van logaritmische schaal:schaal van Richter en chemische pH

Richterschaal

Een bijna perfecte analogie met de belschaal is de schaal van Richter die wordt gebruikt om de intensiteit van de aardbeving te beschrijven:een aardbeving van 6.0 Richter is 10 keer krachtiger dan een aardbeving van 5.0 Richter; een aardbeving van 7,0 Richter die 100 keer krachtiger is dan een aardbeving van 5,0 Richter; een aardbeving van 4,0 Richter is 1/10 zo krachtig als een aardbeving van 5,0 Richter, enzovoort.

Chemische pH

De meetschaal voor chemische pH is eveneens logaritmisch, een verschil van 1 op de schaal komt overeen met een tienvoudig verschil in waterstofionenconcentratie van een chemische oplossing. Een voordeel van het gebruik van een logaritmische meetschaal is het enorme expressiebereik dat wordt geboden door een relatief kleine reeks numerieke waarden, en het is dit voordeel dat het gebruik van Richter-getallen voor aardbevingen en pH voor waterstofionenactiviteit verzekert.

De Bel gebruiken om systeemwinsten en -verliezen uit te drukken

Een andere reden voor het gebruik van de bel als een eenheid voor winst is de eenvoudige uitdrukking van systeemwinsten en -verliezen. Beschouw het laatste systeemvoorbeeld (figuur hierboven) waar twee versterkers tandem zijn aangesloten om een ​​signaal te versterken. De respectieve versterking voor elke versterker werd uitgedrukt als een verhouding, en de totale versterking voor het systeem was het product (vermenigvuldiging) van die twee verhoudingen:

Algemene winst =(3)(5) =15

Als deze cijfers macht vertegenwoordigen versterkingen, kunnen we de eenheid van bel direct toepassen op de taak om de versterking van elke versterker en van het systeem in zijn geheel weer te geven. (Figuur hieronder)

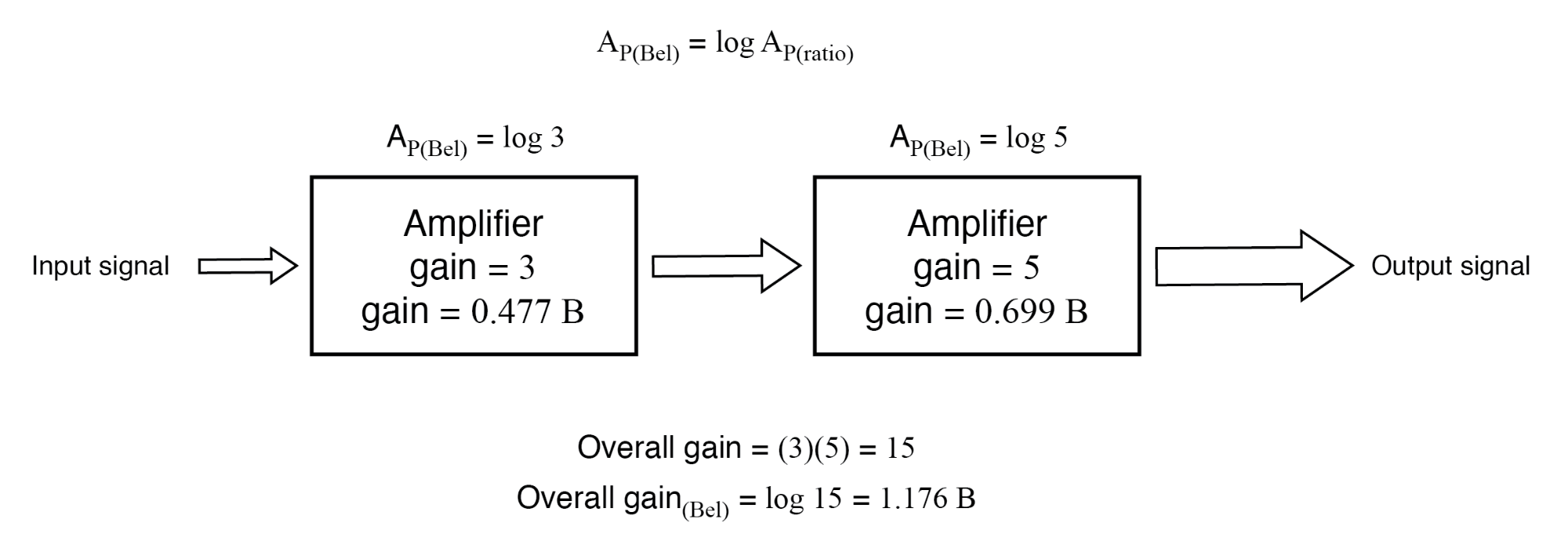
Vermogenswinst in bels is additief:0,477 B + 0,699 B =1,176 B.

Nauwkeurige inspectie van deze winstcijfers in de eenheid "bel" levert een ontdekking op:ze zijn additief. Verhoudingsversterkingscijfers zijn multiplicatief voor getrapte versterkers, maar versterkingen uitgedrukt in bels add in plaats van vermenigvuldigen om de totale systeemwinst te evenaren. De eerste versterker met zijn vermogensversterking van 0,477 B draagt ​​bij aan de vermogensversterking van de tweede versterker van 0,699 B om een ​​systeem te maken met een totale vermogensversterking van 1,176 B.

Winst bij gebruik van decibel

Als we herberekenen voor decibel in plaats van bels, zien we hetzelfde fenomeen. (Figuur hieronder)

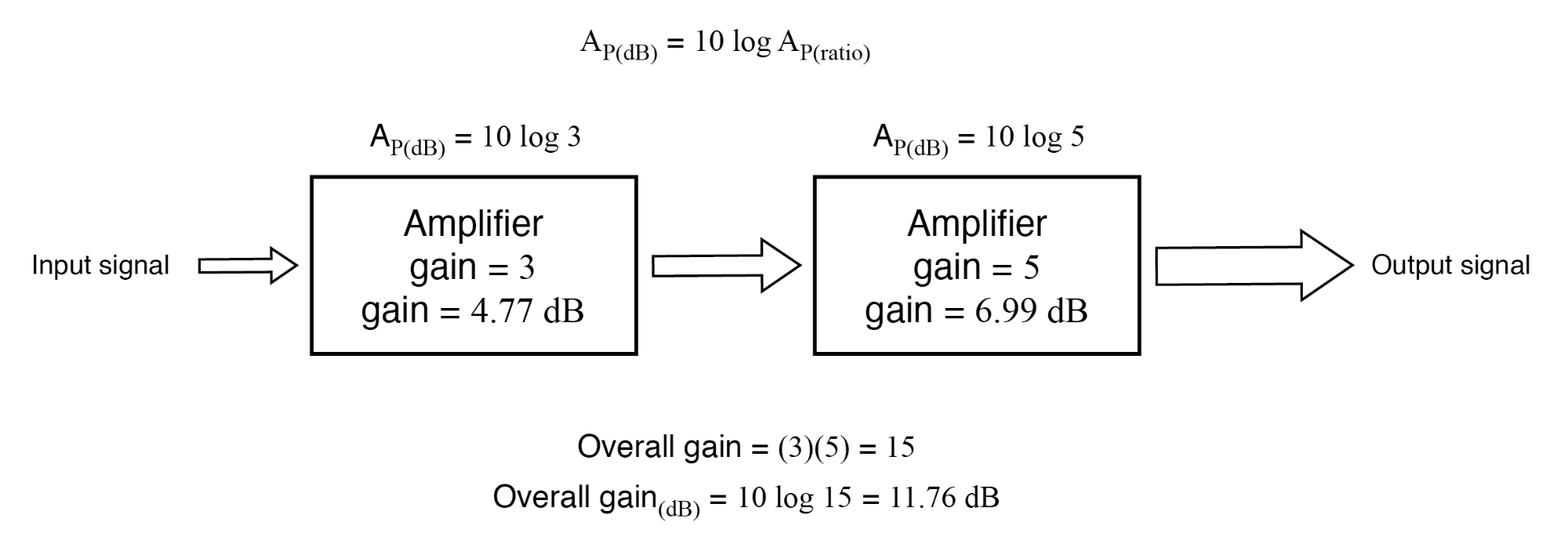
Versterking van versterkertrappen in decibel is additief:4,77 dB + 6,99 dB =11,76 dB.

Voor degenen die al bekend zijn met de rekenkundige eigenschappen van logaritmen, is dit geen verrassing. Het is een elementaire regel van de algebra dat de antilogaritme van de som van de logaritmewaarden van twee getallen gelijk is aan het product van de twee oorspronkelijke getallen. Met andere woorden, als we twee getallen nemen en de logaritme van elk bepalen, dan die twee logaritmecijfers bij elkaar optellen en dan de "antilogaritme" van die som bepalen (verhoog het grondtal van de logaritme - in dit geval 10 - tot de macht van die som), zal het resultaat hetzelfde zijn alsof we de twee originele getallen gewoon met elkaar hadden vermenigvuldigd.

Deze algebraïsche regel vormt het hart van een apparaat dat een schuifregel wordt genoemd , een analoge computer die, onder andere, de producten en quotiënten van getallen kan bepalen door optellen (het optellen van fysieke lengtes die zijn gemarkeerd op glijdende houten, metalen of plastic schalen).

Gegeven een tabel met logaritmecijfers, zou dezelfde wiskundige truc kunnen worden gebruikt om anders complexe vermenigvuldigingen en delingen uit te voeren door alleen respectievelijk optellen en aftrekken te doen. Met de komst van snelle, draagbare, digitale rekenmachines, verdween deze elegante rekentechniek vrijwel uit het populaire gebruik. Het is echter nog steeds belangrijk om te begrijpen wanneer u werkt met meetschalen die logaritmisch van aard zijn, zoals de bel (decibel) en de schaal van Richter.

Conversie van Decibel en Unitless Ratio

Bij het converteren van een vermogenswinst van eenheden van bels of decibel naar een eenheidsloze verhouding, wordt de wiskundige inverse functie van gewone logaritmen gebruikt:machten van 10, of de antilog .

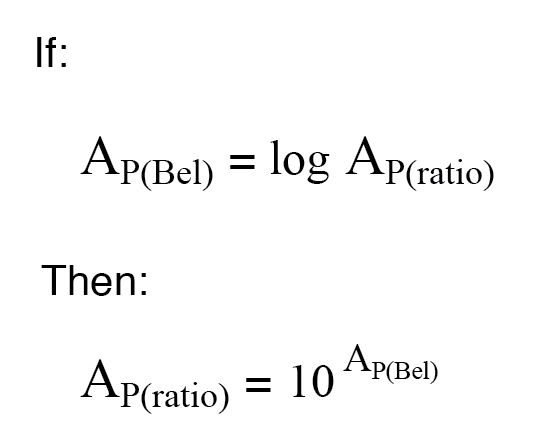
Het omzetten van decibel naar eenheidsloze verhoudingen voor vermogenswinst is vrijwel hetzelfde, alleen een delingsfactor van 10 is opgenomen in de exponentterm:

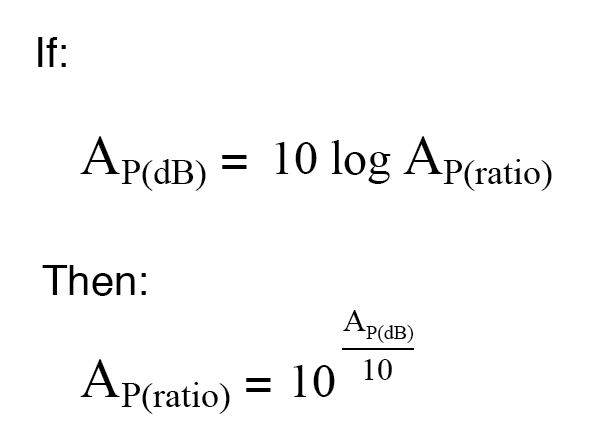
Voorbeeld: Het vermogen in een versterker is 1 Watt, het uitgangsvermogen is 10 Watt. Vind de vermogenswinst in dB.

AP(dB) =10*log10(PO / PI) =10*log10(10 /1) =10*log10(10) =10*(1) =10 dB

Voorbeeld: Zoek de vermogensversterkingsverhouding AP(ratio) =(PO / PI) voor een vermogensversterking van 20 dB.

AP(dB) =20 =10*log10(APratio ) 20/10 =log10*(APratio ) 10^(20/10) =10^(log10*(APratio )) 10^2 =100 =AP(ratio) =(PO / PI)

Omzetten van vermogensversterking naar spannings-/stroomversterking

Omdat de bel in wezen een eenheid is van kracht winst of verlies in een systeem, spannings- of stroomwinsten en -verliezen worden niet op dezelfde manier omgezet in bels of dB. Wanneer we bels of decibels gebruiken om een ​​andere winst dan vermogen uit te drukken, of het nu spanning of stroom is, moeten we de berekening uitvoeren in termen van hoeveel vermogenswinst er zou zijn voor die hoeveelheid spanning of stroomversterking.

Voor een constante belastingsimpedantie komt een spannings- of stroomversterking van 2 overeen met een vermogensversterking van 4 (2 ² ); een spannings- of stroomversterking van 3 komt overeen met een vermogensversterking van 9 (3 ² ). Als we spanning of stroom vermenigvuldigen met een bepaalde factor, dan is de vermogenswinst die door die vermenigvuldiging wordt veroorzaakt, het kwadraat van die factor. Dit heeft betrekking op de vormen van de wet van Joule, waarbij het vermogen werd berekend op basis van spanning of stroom en weerstand:

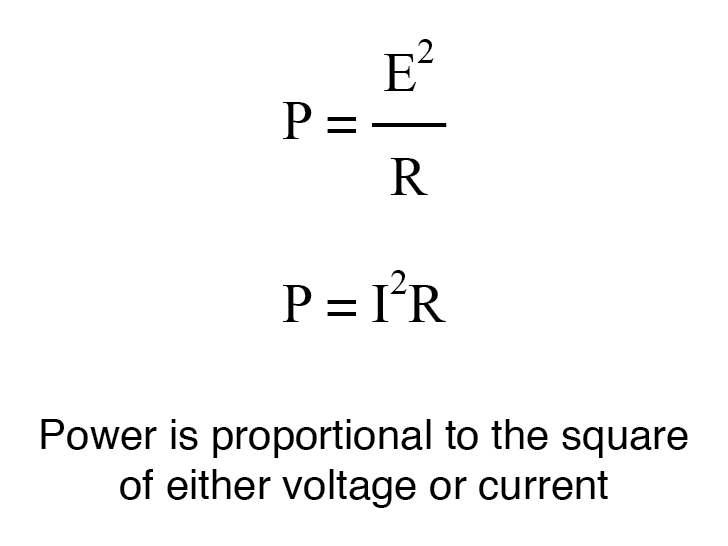
Dus bij het vertalen van een spannings- of stroomversterkingsfactor ratio in een respectieve winst in termen van de bel-eenheid, moeten we deze exponent opnemen in de vergelijking(en):

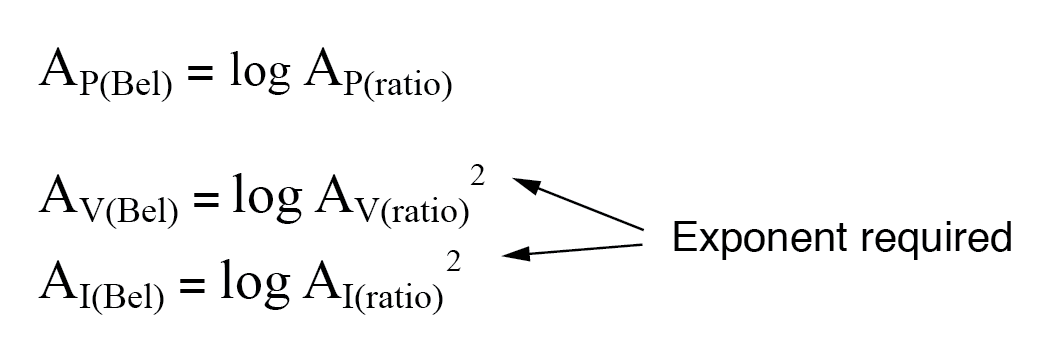
Dezelfde exponentvereiste geldt bij het uitdrukken van spannings- of stroomwinsten in decibel:

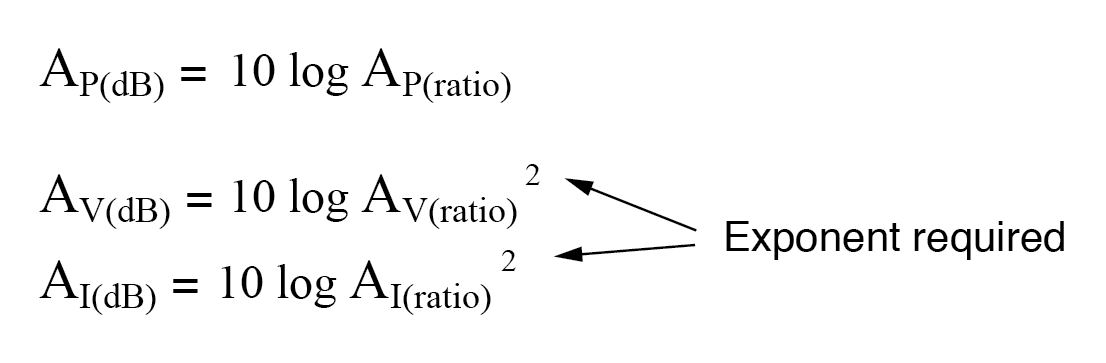
Dankzij een andere interessante eigenschap van logaritmen kunnen we deze vergelijkingen vereenvoudigen om de exponent te elimineren door de "2" op te nemen als een vermenigvuldigingsfactor voor de logaritmefunctie. Met andere woorden, in plaats van de logaritme van het vierkant te nemen van de spannings- of stroomversterking, vermenigvuldigen we het logaritme van de spannings- of stroomversterking met 2 en het uiteindelijke resultaat in bels of decibel zal hetzelfde zijn:

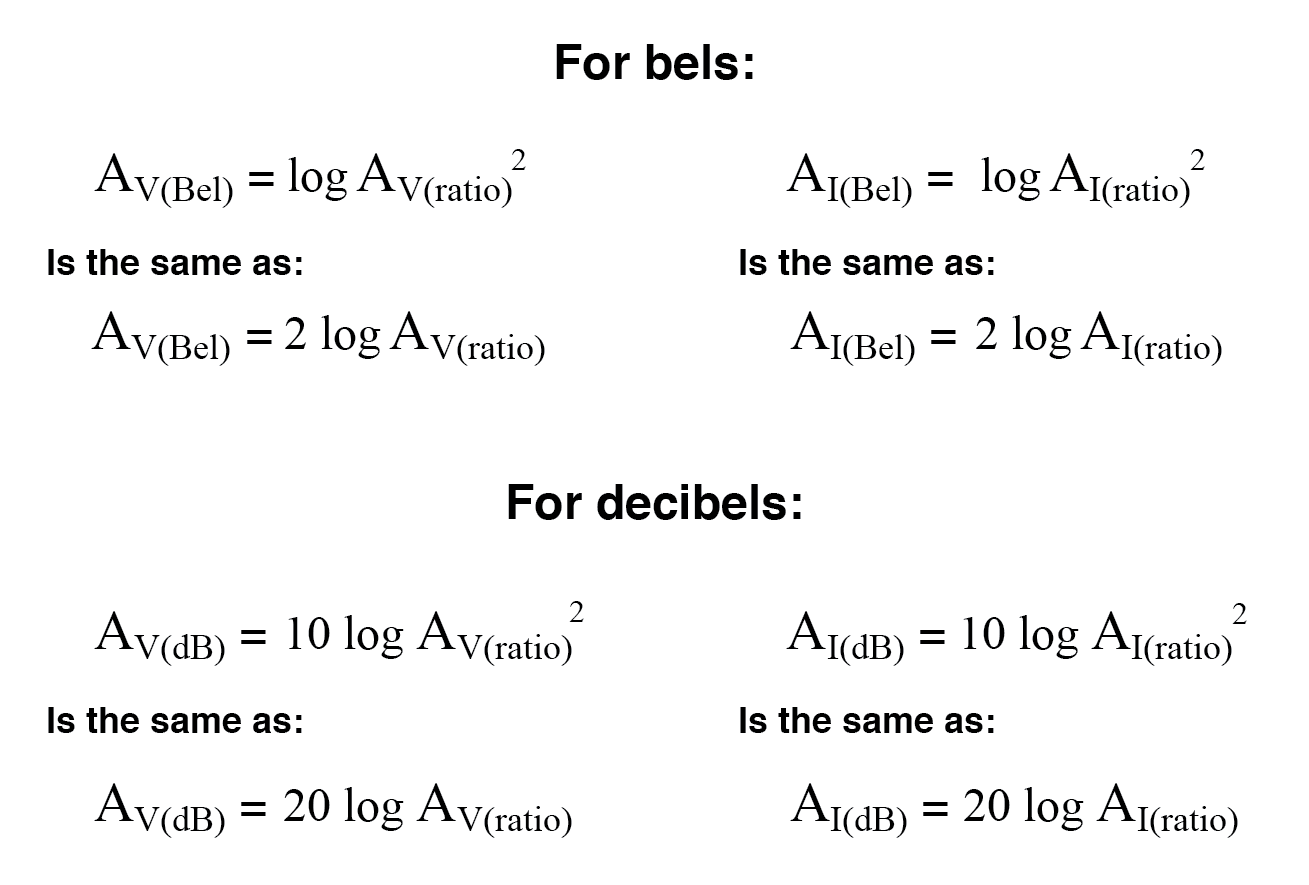
Het proces van het omzetten van spannings- of stroomwinsten van bels of decibels in eenheidsloze verhoudingen is vrijwel hetzelfde als voor vermogenswinsten:

Hier zijn de vergelijkingen die worden gebruikt om spannings- of stroomwinsten in decibel om te zetten in eenheidsloze verhoudingen:

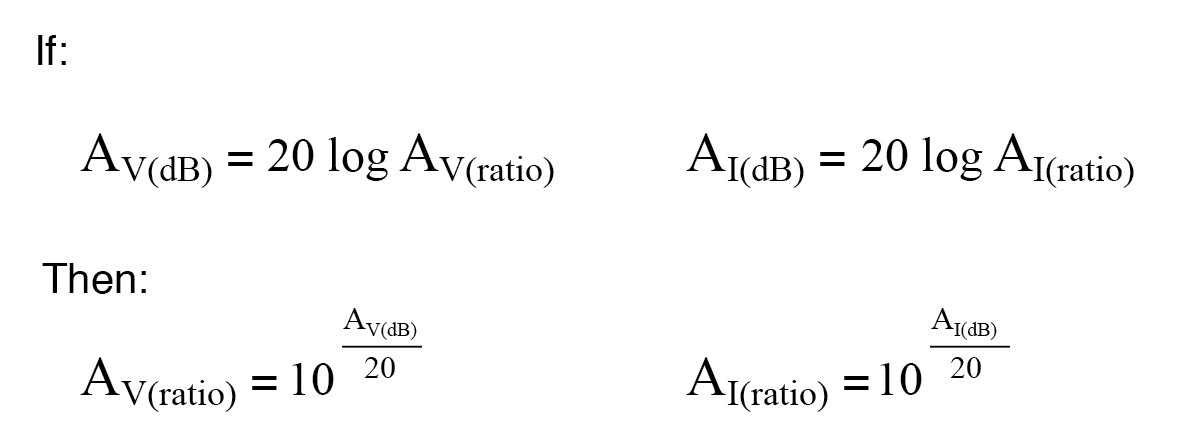
Hoewel de bel een eenheid is die van nature is geschaald voor vermogen, is er een andere logaritmische eenheid uitgevonden om spannings- of stroomwinsten/verliezen direct uit te drukken, en deze is gebaseerd op de natuurlijke logaritme in plaats van de gewone logaritme zoals bels en decibellen zijn. Riep de neper , het eenheidssymbool is "Np; er kunnen echter kleine letters "n" voorkomen.

Ten goede of ten kwade, noch de neper, noch zijn verzwakte neef, de decineper , wordt in de volksmond gebruikt als een eenheid in Amerikaanse technische toepassingen. Voorbeeld: De spanning in een audiolijnversterker van 600 is 10 mV, de spanning over een belasting van 600 Ω is 1 V. Zoek de vermogenswinst in dB.

A(dB) =20 log10(VO / VI) =20 log10 (1 /0,01) =20 log10 (100) =20 (2) =40 dB

Voorbeeld: Vind de spanningsversterkingsverhouding AV(ratio) =(VO / VI) voor een 20 dB versterkingsversterker met een ingangs- en uitgangsimpedantie van 50 Ω.

AV(dB) =20 log10 AV(ratio) 20 =20 log10 AV(ratio) 20/20 =log10 AP(ratio) 1020/20 =10log10 (AV(ratio)) 10 =AV(ratio) =( VO / VI)

Een overzicht van de decibel

• Winsten en verliezen kunnen worden uitgedrukt in termen van een eenheidsloze verhouding, of in de eenheid van bels (B) of decibel (dB). Een decibel is letterlijk een deci -bel:een tiende van een bel.
• De bel is in wezen een eenheid voor het uitdrukken van kracht winst of verlies. Gebruik een van deze vergelijkingen om een ​​vermogensverhouding om te zetten in bels of decibels:

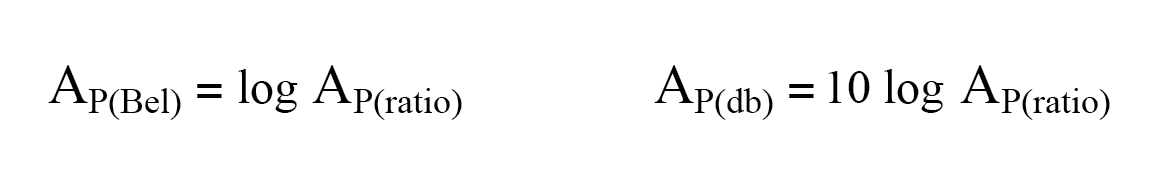
• Bij gebruik van de eenheid bel of decibel om een ​​spanning uit te drukken of huidig verhouding, moet het worden gegoten in termen van een equivalent vermogen verhouding. Praktisch betekent dit het gebruik van verschillende vergelijkingen, met een vermenigvuldigingsfactor van 2 voor de logaritmewaarde die overeenkomt met een exponent van 2 voor de spannings- of stroomversterkingsverhouding:

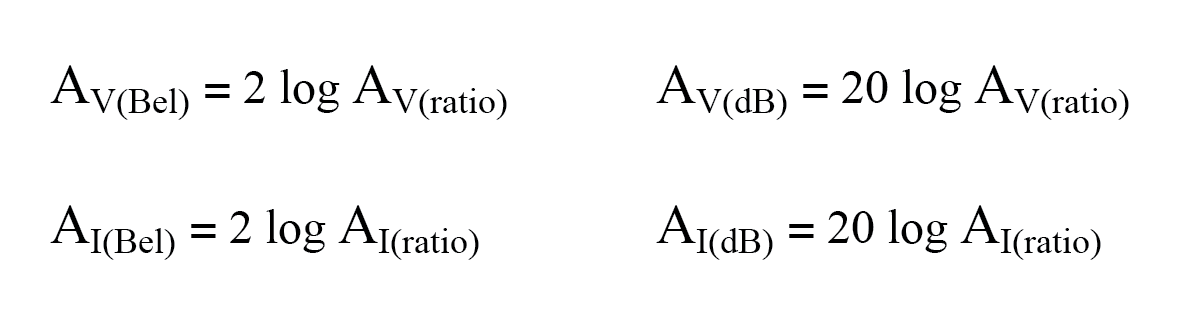
• Gebruik een van deze vergelijkingen om een ​​decibelversterking om te zetten in een eenheidsloze verhoudingsversterking:

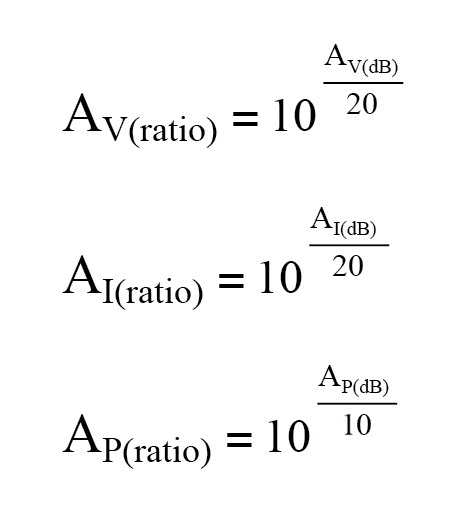
• Een versterking (versterking) wordt uitgedrukt als een positief bel- of decibelcijfer. Een verlies (demping) wordt uitgedrukt als een negatief bel- of decibelcijfer. Eenheidswinst (geen winst of verlies; verhouding =1) wordt uitgedrukt als nul bels of nul decibel.
• Bij het berekenen van de algehele versterking voor een versterkersysteem dat is samengesteld uit meerdere versterkertrappen, worden de afzonderlijke versterkingsverhoudingen vermenigvuldigd om de algehele versterkingsratio te vinden. Bel- of decibelcijfers voor elke versterkertrap worden daarentegen toegevoegd samen om de totale winst te bepalen.

GERELATEERDE WERKBLAD:

• Werkblad decibelmetingen
• Werkblad elementaire versterkertheorie