Inleiding tot gecombineerde logische functies

De term 'combinatie' komt uit de wiskunde naar ons toe. In de wiskunde is een combinatie een ongeordende set, wat een formele manier is om te zeggen dat het niemand kan schelen in welke volgorde de items binnenkomen. De meeste spellen werken op deze manier, als je één voor één dobbelstenen gooit en een 2 krijgt, gevolgd door een 3, is het hetzelfde alsof je een 3 had gegooid gevolgd door een 2. Met combinatorische logica produceert het circuit dezelfde uitvoer, ongeacht de volgorde waarin de ingangen worden gewijzigd.

Er zijn circuits die afhankelijk zijn van wanneer de ingangen veranderen, deze circuits worden sequentiële logica genoemd. Hoewel je de term "sequentiële logica" niet zult vinden in de titels van de hoofdstukken, zullen de volgende hoofdstukken de sequentiële logica bespreken.

Praktische circuits hebben een mix van combinatorische en sequentiële logica, met sequentiële logica die ervoor zorgt dat alles in de juiste volgorde gebeurt en combinatorische logica die functies uitvoert zoals rekenen, logica of conversie.

U hebt al combinatorische circuits gebruikt. Elke eerder besproken logische poort is een combinatorische logische functie. Laten we volgen hoe twee NAND-poorten werken als we ze in verschillende volgorde invoeren.

We beginnen met beide ingangen die 0 zijn.

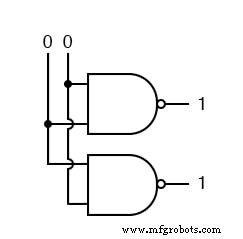
We zetten dan één ingang hoog.

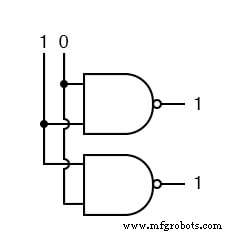
We zetten dan de andere input hoog.

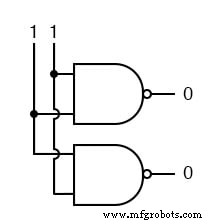
Dus NAND-poorten geven niet om de volgorde van de ingangen, en u zult hetzelfde gedrag aantreffen bij alle andere poorten die tot nu toe zijn behandeld (AND, XOR, OR, NOR, XNOR en NOT).

GERELATEERD WERKBLAD:

• Booleaanse algebra-werkblad