Frequentie- en fasemeting

Een belangrijke elektrische grootheid zonder equivalent in DC-circuits is frequentie .

Frequentiemeting is erg belangrijk in veel toepassingen van wisselstroom, vooral in wisselstroomsystemen die zijn ontworpen om efficiënt te werken op één frequentie en slechts op één frequentie.

Als de wisselstroom wordt gegenereerd door een elektromechanische dynamo, is de frequentie recht evenredig met de assnelheid van de machine en kan de frequentie worden gemeten door eenvoudig de snelheid van de as te meten.

Als de frequentie echter op enige afstand van de dynamo moet worden gemeten, zijn andere meetmethoden nodig.

Methode voor frequentiemeting

Het principe van mechanische resonantie gebruiken

Een eenvoudige maar grove methode voor frequentiemeting in energiesystemen maakt gebruik van het principe van mechanische resonantie. Elk fysiek object dat de eigenschap van elasticiteit (veerkracht) bezit, heeft een inherente frequentie waarmee het de voorkeur geeft om te trillen.

De stemvork is hier een goed voorbeeld van:sla er één keer op en hij zal blijven trillen op een toon die specifiek is voor zijn lengte. Langere stemvorken hebben lagere resonantiefrequenties:hun tonen zullen lager zijn op de toonladder dan kortere vorken.

Stel je een rij van steeds groter wordende stemvorken voor die naast elkaar zijn gerangschikt. Ze zijn allemaal op een gemeenschappelijke basis gemonteerd en die basis wordt door middel van een elektromagneet in trilling gebracht met de frequentie van de gemeten wisselspanning (of stroom).

De stemvork die qua resonantiefrequentie het dichtst bij de frequentie van die trilling ligt, zal de neiging hebben om het meest (of het luidst) te trillen. Als de tanden van de vorken dun genoeg waren, zouden we de relatieve beweging van elk kunnen zien door de lengte van de vervaging die we zouden zien als we ze allemaal vanuit een eindaanzicht inspecteerden.

Nou, maak een verzameling "stemvorken" van een strook plaatstaal gesneden in een patroon dat lijkt op een hark, en je hebt het trillende riet frequentiemeter:

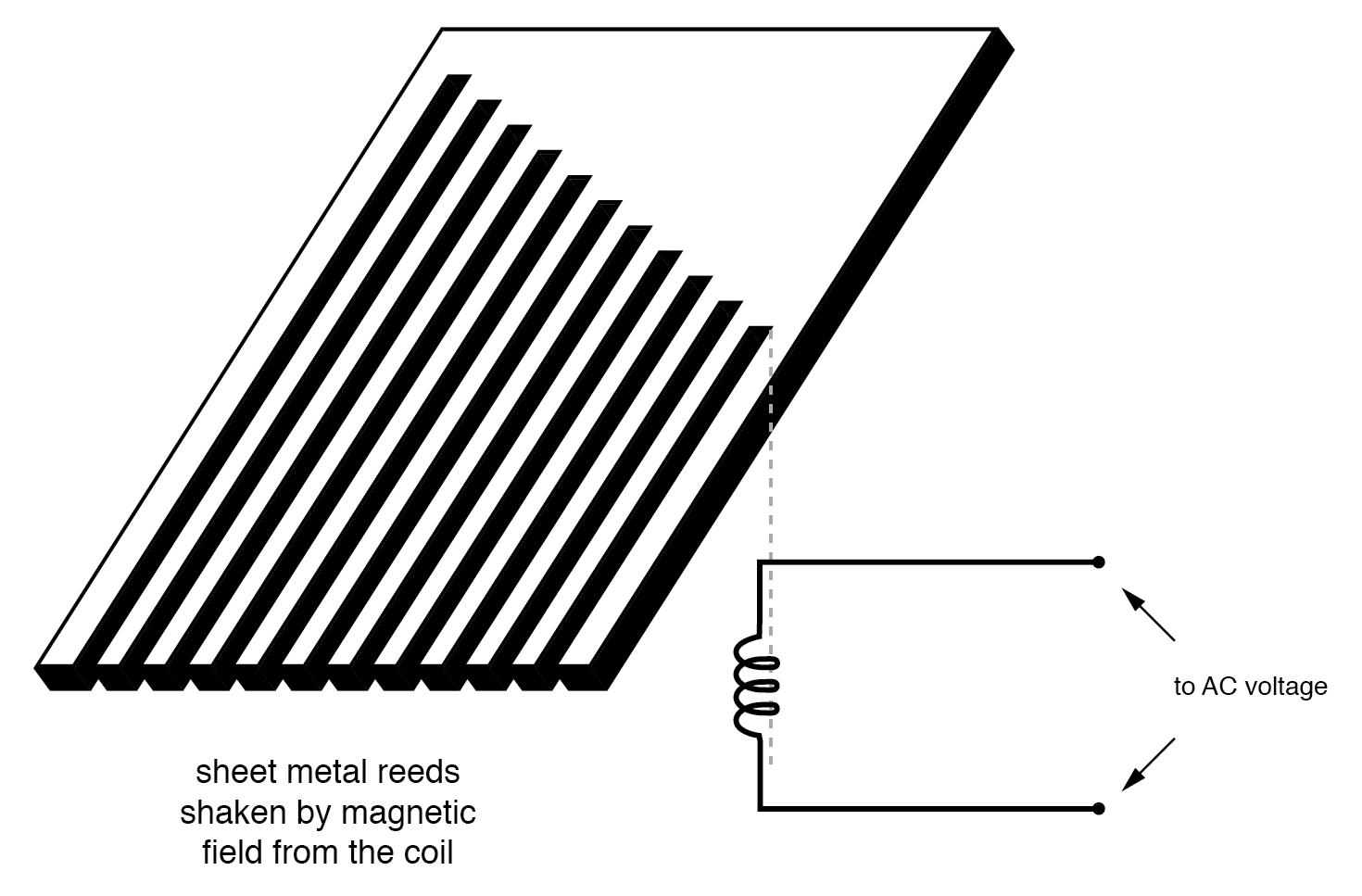
Trillend rietfrequentiemeterdiagram.

De gebruiker van deze meter bekijkt de uiteinden van al die rieten van ongelijke lengte terwijl ze collectief worden geschud met de frequentie van de aangelegde wisselspanning op de spoel. Degene die qua resonantiefrequentie het dichtst bij de toegepaste wisselstroom ligt, trilt het meest, en ziet er ongeveer zo uit:

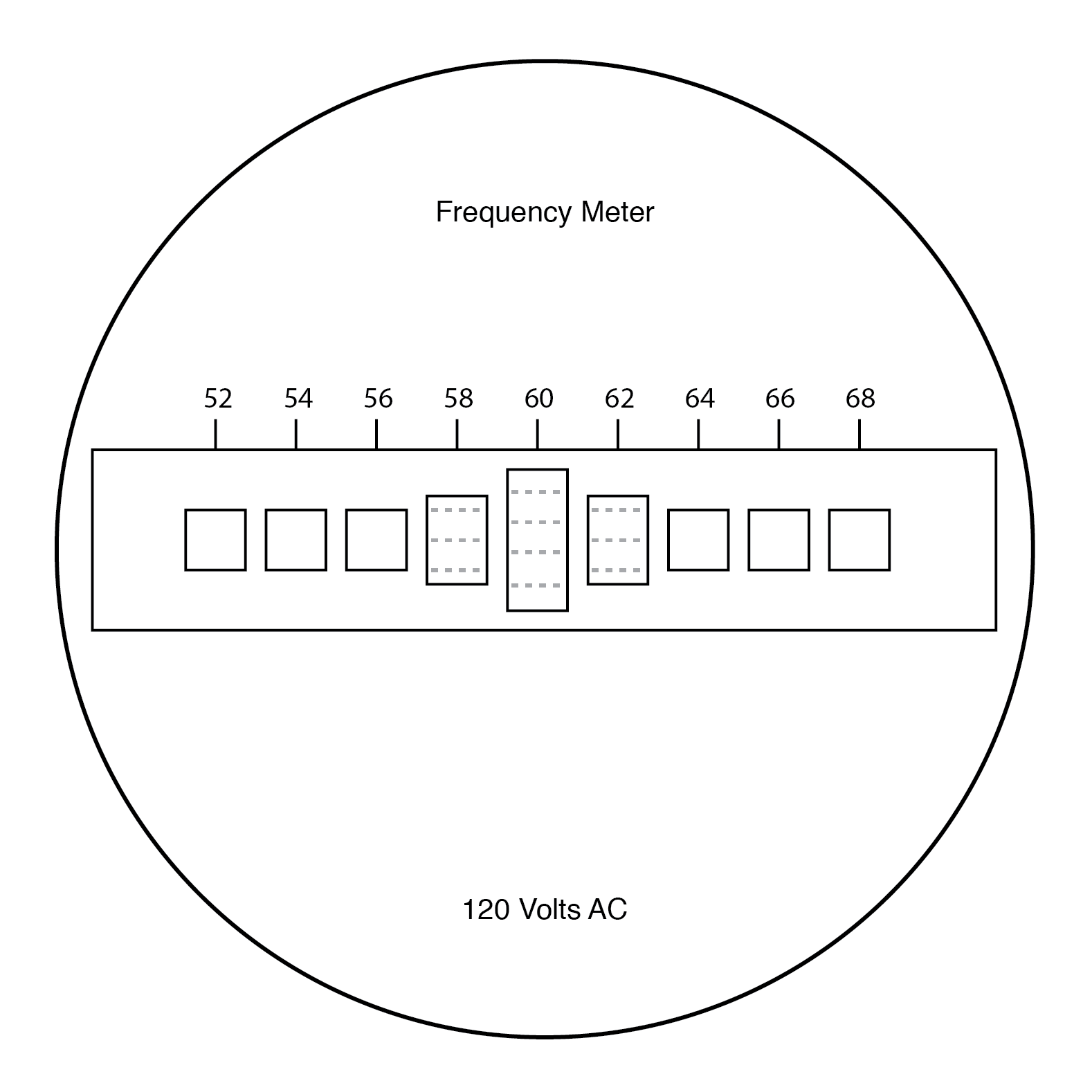
Voorpaneel van vibrerende rietfrequentiemeter.

Trillende rietmeters zijn natuurlijk geen precisie-instrumenten, maar ze zijn heel eenvoudig en daarom gemakkelijk te vervaardigen om robuust te zijn. Ze worden vaak aangetroffen op kleine, door een motor aangedreven generatorsets om het motortoerental zo in te stellen dat de frequentie iets in de buurt komt van 60 (50 in Europa) Hertz.

Een vorm van tankcircuit gebruiken

Hoewel riet-type meters onnauwkeurig zijn, is hun werkingsprincipe dat niet. In plaats van mechanische resonantie kunnen we elektrische resonantie vervangen door een frequentiemeter te ontwerpen met een spoel en condensator in de vorm van een tankcircuit (parallelle spoel en condensator). Zie onderstaande afbeelding.

Een of beide componenten zijn instelbaar gemaakt en er is een meter in het circuit geplaatst om de maximale amplitude van de spanning over de twee componenten aan te geven.

De instelknop(pen) zijn gekalibreerd om de resonantiefrequentie voor een bepaalde instelling weer te geven, en de frequentie wordt ervan afgelezen nadat het apparaat is aangepast voor de maximale indicatie op de meter.

In wezen is dit een afstembaar filtercircuit dat wordt aangepast en vervolgens wordt gelezen op een manier die vergelijkbaar is met een brugcircuit (dat moet worden gebalanceerd voor een "nul"-toestand en vervolgens moet worden gelezen).

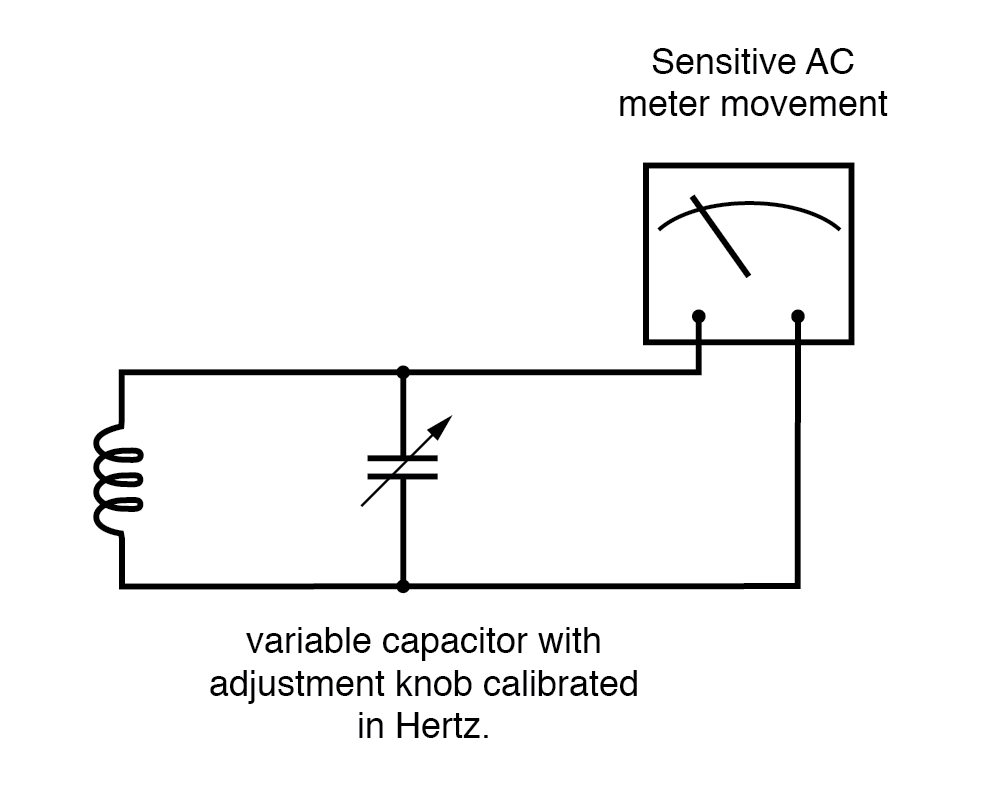
Resonantiefrequentiemeter "piekt" wanneer de LC-resonantiefrequentie wordt afgestemd om de frequentie te testen.

Deze techniek is populair bij radioamateurs (of dat was het in ieder geval vóór de komst van goedkope digitale frequentie-instrumenten die tellers worden genoemd. ), vooral omdat er geen directe verbinding met het circuit nodig is.

Zolang de spoel en/of condensator voldoende strooiveld (respectievelijk magnetisch of elektrisch) van het te testen circuit kunnen onderscheppen om de meter te laten aangeven, zal het werken.

Net als bij andere soorten elektrische metingen, zijn de meest nauwkeurige meetmethoden meestal die waarbij een onbekende hoeveelheid wordt vergeleken met een bekende standaard , het basisinstrument doet niets anders dan aangeven wanneer de twee grootheden aan elkaar gelijk zijn.

Dit is het basisprincipe achter het DC (Wheatstone) brugcircuit en het is een degelijk metrologisch principe dat in de hele wetenschappen wordt toegepast. Als we toegang hebben tot een nauwkeurige frequentiestandaard (een bron van wisselspanning die zeer nauwkeurig op een enkele frequentie past), zou het meten van een onbekende frequentie relatief eenvoudig moeten zijn.

Kwartskristal gebruiken

Voor die frequentiestandaard richten we onze aandacht weer op de stemvork, of op zijn minst een modernere variant daarvan genaamd het kwartskristal .

Kwarts is een natuurlijk voorkomend mineraal met een zeer interessante eigenschap genaamd piëzo-elektriciteit . Piëzo-elektrische materialen produceren een spanning over hun lengte wanneer ze fysiek worden belast, en zullen fysiek vervormen wanneer een externe spanning over hun lengte wordt aangelegd.

Deze vervorming is in de meeste gevallen zeer, zeer gering, maar ze bestaat wel.

Kwartsgesteente is elastisch (veerkrachtig) binnen dat kleine buigingsbereik dat een externe spanning zou produceren, wat betekent dat het een eigen mechanische resonantiefrequentie zal hebben die zich kan manifesteren als een elektrisch spanningssignaal.

Met andere woorden, als een kwartschip wordt geraakt, zal deze "rinkelen" met zijn eigen unieke frequentie die wordt bepaald door de lengte van de chip, en die resonante oscillatie zal een equivalente spanning produceren over meerdere punten van de kwartschip die kan worden afgetapt in door draden die aan het oppervlak van de chip zijn bevestigd.

Op een wederzijdse manier zal de kwartschip de neiging hebben om het meest te trillen wanneer deze wordt "opgewonden" door een aangelegde wisselspanning met precies de juiste frequentie, net als de tongen op een vibrerende rietfrequentiemeter.

Chips van kwartsgesteente kunnen precies worden gesneden voor de gewenste resonantiefrequenties, en die chip kan stevig in een beschermende schaal worden gemonteerd met draden die zich uitstrekken voor aansluiting op een extern elektrisch circuit.

Als het als zodanig is verpakt, wordt het resulterende apparaat eenvoudig een kristal genoemd (of soms "xtal ”). Het schematische symbool wordt weergegeven in de onderstaande afbeelding.

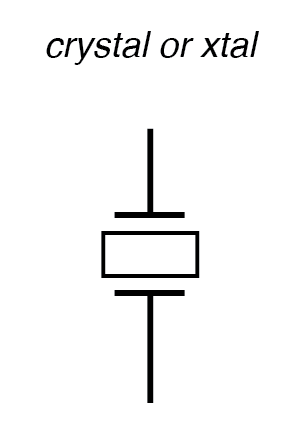
Kristal (frequentiebepalend element) schematisch symbool.

Elektrisch is die kwartschip gelijk aan een serie LC-resonantieschakeling. (Figuur hieronder) De diëlektrische eigenschappen van kwarts dragen een extra capacitief element bij aan het equivalente circuit.

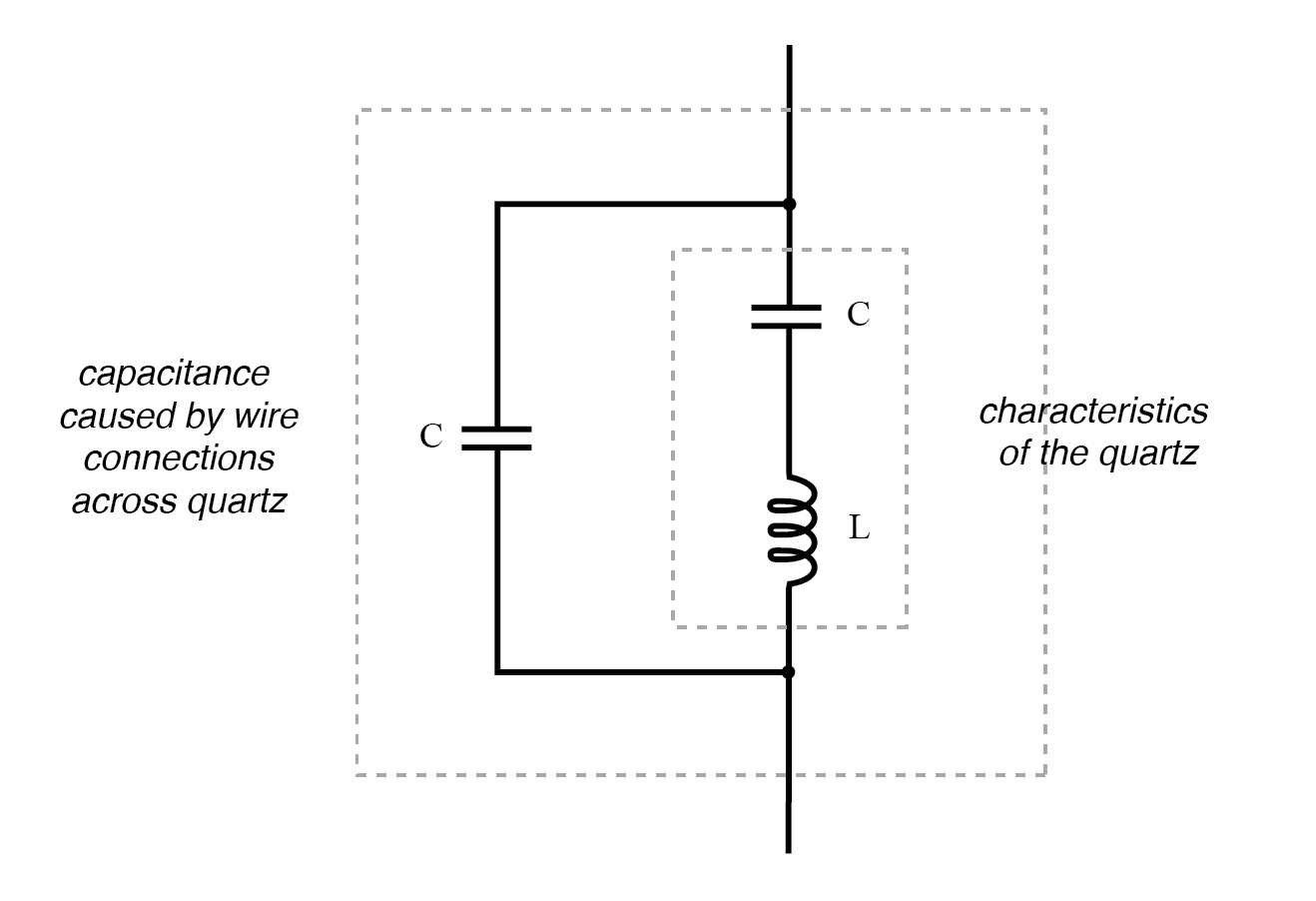
Kwartskristal-equivalent circuit.

De "capaciteit" en "inductantie" die in serie worden getoond, zijn slechts elektrische equivalenten van de mechanische resonantie-eigenschappen van het kwarts:ze bestaan ​​niet als afzonderlijke componenten in het kristal. De parallel weergegeven capaciteit vanwege de draadverbindingen over het diëlektrische (isolerende) kwartslichaam is reëel en heeft een effect op de resonantierespons van het hele systeem.

Een volledige discussie over kristaldynamica is hier niet nodig, maar wat over kristallen moet worden begrepen, is deze resonantiecircuitequivalentie en hoe deze binnen een oscillatorcircuit kan worden benut om een ​​uitgangsspanning te bereiken met een stabiele, bekende frequentie.

Kristallen hebben als resonerende elementen doorgaans een veel hogere "Q" (kwaliteit ) waarden dan tankcircuits die zijn opgebouwd uit inductoren en condensatoren, voornamelijk vanwege de relatieve afwezigheid van strooiweerstand, waardoor hun resonantiefrequenties zeer duidelijk en nauwkeurig zijn.

Omdat de resonantiefrequentie uitsluitend afhankelijk is van de fysieke eigenschappen van kwarts (een zeer stabiele substantie, mechanisch), is de resonantiefrequentievariatie in de tijd met een kwartskristal zeer, zeer laag. Dit is hoe kwartsbeweging horloges verkrijgen hun hoge nauwkeurigheid:door middel van een elektronische oscillator die wordt gestabiliseerd door de resonerende werking van een kwartskristal.

Voor laboratoriumtoepassingen kan echter een nog grotere frequentiestabiliteit gewenst zijn. Om dit te bereiken, kan het kristal in kwestie in een temperatuurgestabiliseerde omgeving (meestal een oven) worden geplaatst, waardoor frequentiefouten als gevolg van thermische uitzetting en samentrekking van het kwarts worden geëlimineerd.

Voor de ultieme frequentiestandaard is er echter niets dat tot nu toe is ontdekt dat de nauwkeurigheid van een enkel resonerend atoom overtreft. Dit is het principe van de zogenaamde atoomklok , die een atoom kwik (of cesium) gebruikt dat in een vacuüm is gesuspendeerd, opgewekt door energie van buitenaf om te resoneren op zijn eigen unieke frequentie.

De resulterende frequentie wordt gedetecteerd als een radiogolfsignaal en dat vormt de basis voor de meest nauwkeurige klokken die de mensheid kent. Nationale standaardlaboratoria over de hele wereld onderhouden enkele van deze hypernauwkeurige klokken en zenden frequentiesignalen uit op basis van de trillingen van die atomen zodat wetenschappers en technici kunnen afstemmen en gebruiken voor frequentiekalibratiedoeleinden.

Praktisch onderdeel

Nu komen we bij het praktische gedeelte:zodra we een bron hebben van nauwkeurige frequentie, hoe vergelijken we dat met een onbekende frequentie om een ​​meting te verkrijgen?

Een manier is om een ​​beeldbuis te gebruiken als een frequentievergelijkingsapparaat. Kathodestraalbuizen hebben typisch middelen om de elektronenbundel zowel in de horizontale als in de verticale as af te buigen.

Als metalen platen worden gebruikt om de elektronen elektrostatisch af te buigen, is er een paar platen links en rechts van de straal, evenals een paar platen boven en onder de straal, zoals in de onderstaande afbeelding.

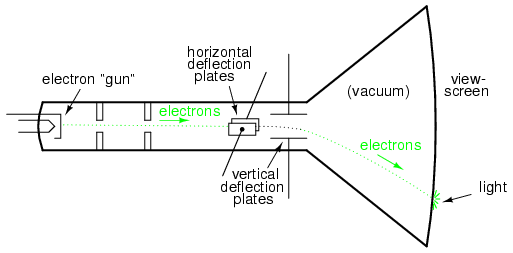
Kathodestraalbuis (CRT) met verticale en horizontale afbuigplaten.

Als we één wisselstroomsignaal toestaan ​​om de straal op en neer af te buigen (sluit die wisselspanningsbron aan op de "verticale" afbuigplaten) en een ander wisselstroomsignaal om de straal naar links en rechts af te buigen (met behulp van het andere paar afbuigplaten), zullen patronen worden geproduceerd op het scherm van de CRT indicatief voor de verhouding van deze twee AC-frequenties.

Deze patronen heten Lissajous-figuren en zijn een veelgebruikt middel voor vergelijkende frequentiemeting in de elektronica.

Als de twee frequenties hetzelfde zijn, krijgen we een eenvoudig cijfer op het scherm van de CRT, waarbij de vorm van dat cijfer afhankelijk is van de faseverschuiving tussen de twee AC-signalen. Hier is een steekproef van Lissajous-cijfers voor twee sinusgolfsignalen van gelijke frequentie, weergegeven zoals ze zouden verschijnen op het gezicht van een oscilloscoop (een AC-spanningsmeetinstrument dat een CRT als zijn "beweging" gebruikt).

De eerste foto is van de Lissajous-figuur gevormd door twee wisselspanningen die perfect in fase met elkaar zijn:

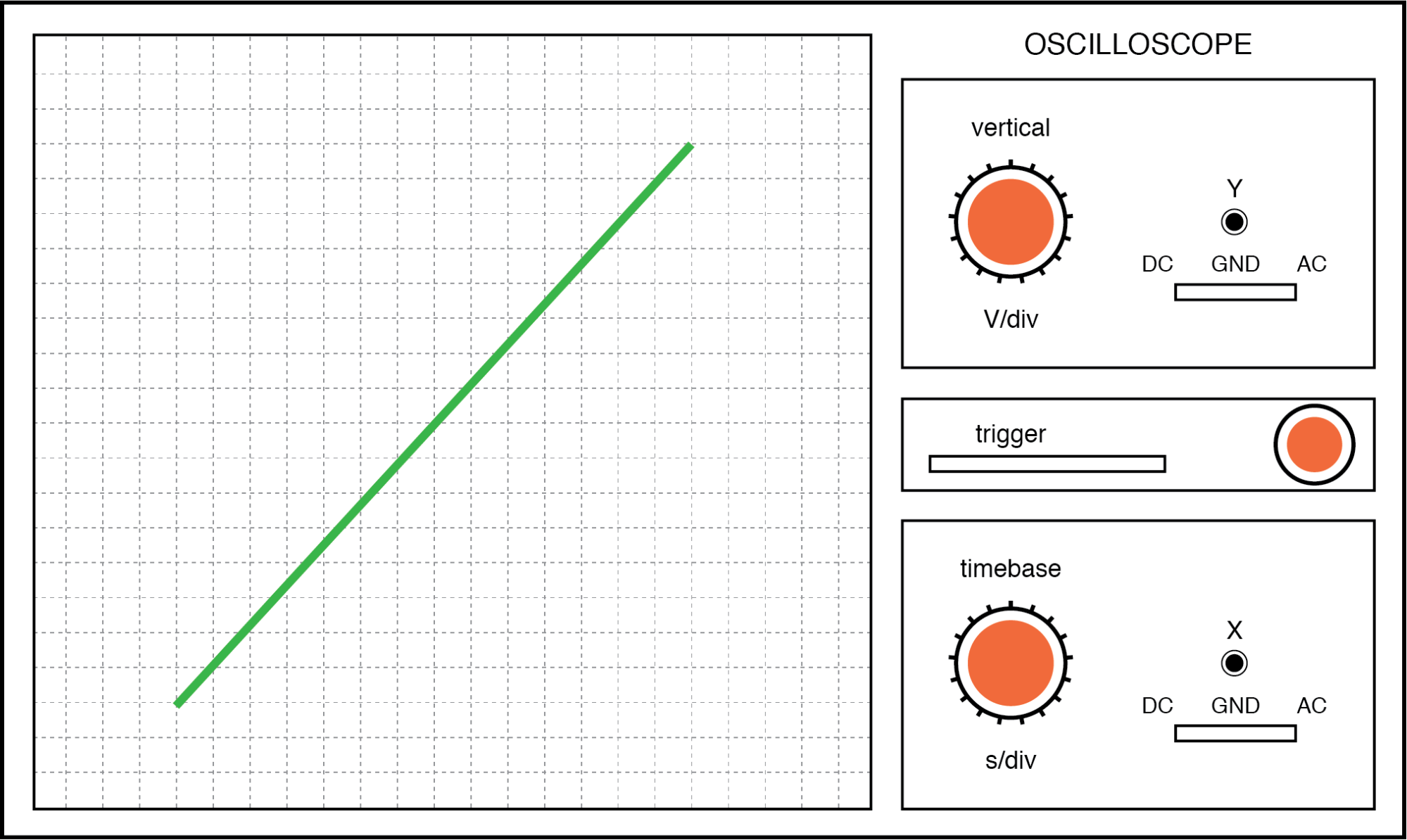
Lissajous-figuur:zelfde frequentie, nul graden faseverschuiving.

Als de twee wisselspanningen niet in fase met elkaar zijn, wordt er geen rechte lijn gevormd. In plaats daarvan zal de Lissajous-figuur het uiterlijk van een ovaal krijgen en perfect cirkelvormig worden als de faseverschuiving precies 90° is tussen de twee signalen en als hun amplituden gelijk zijn:

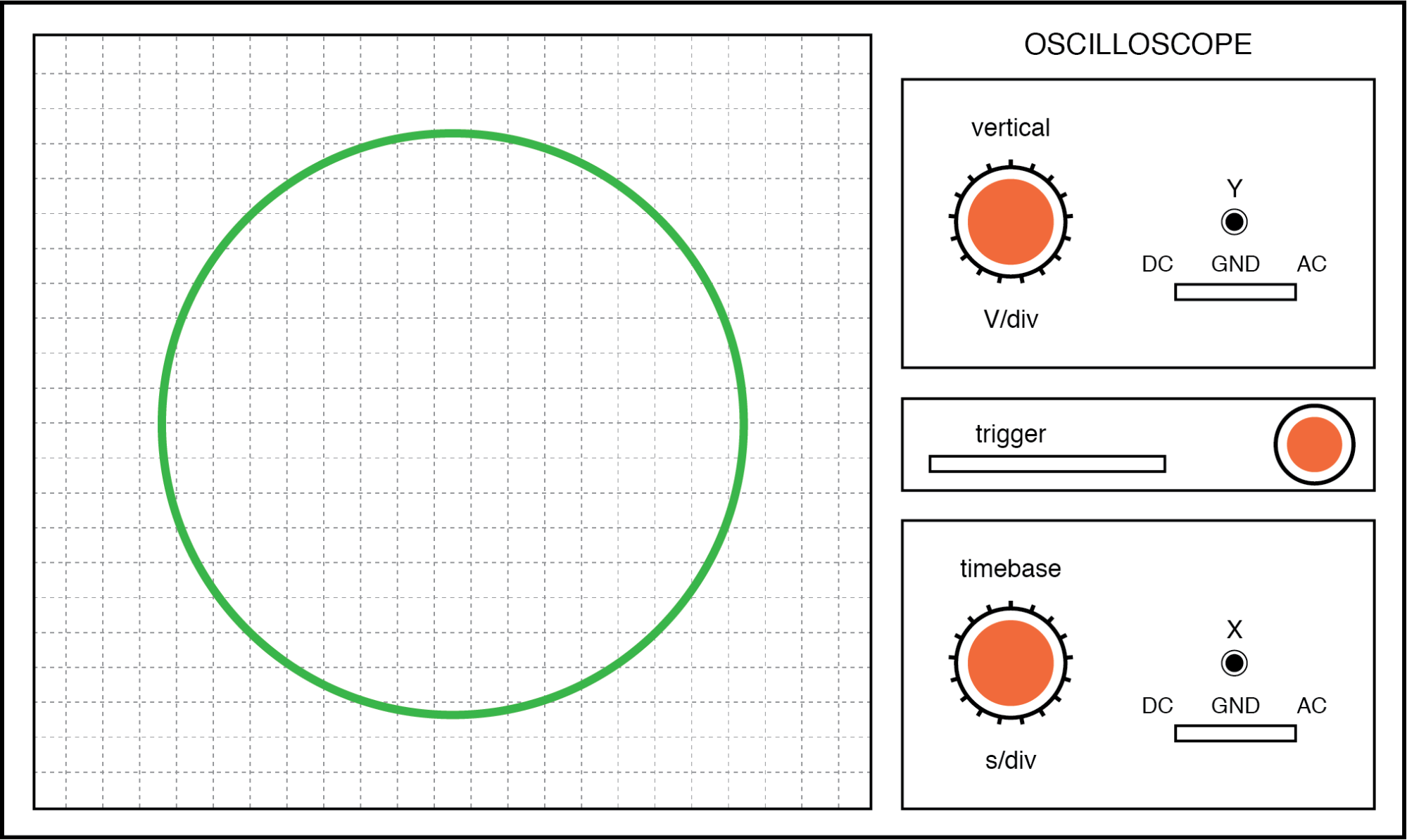
Lissajous-figuur:zelfde frequentie, 90 of 270 graden faseverschuiving.

Ten slotte, als de twee AC-signalen in fase direct tegenover elkaar staan ​​(180° verschuiving), krijgen we weer een lijn, maar deze keer zal deze in de tegenovergestelde richting worden georiënteerd:

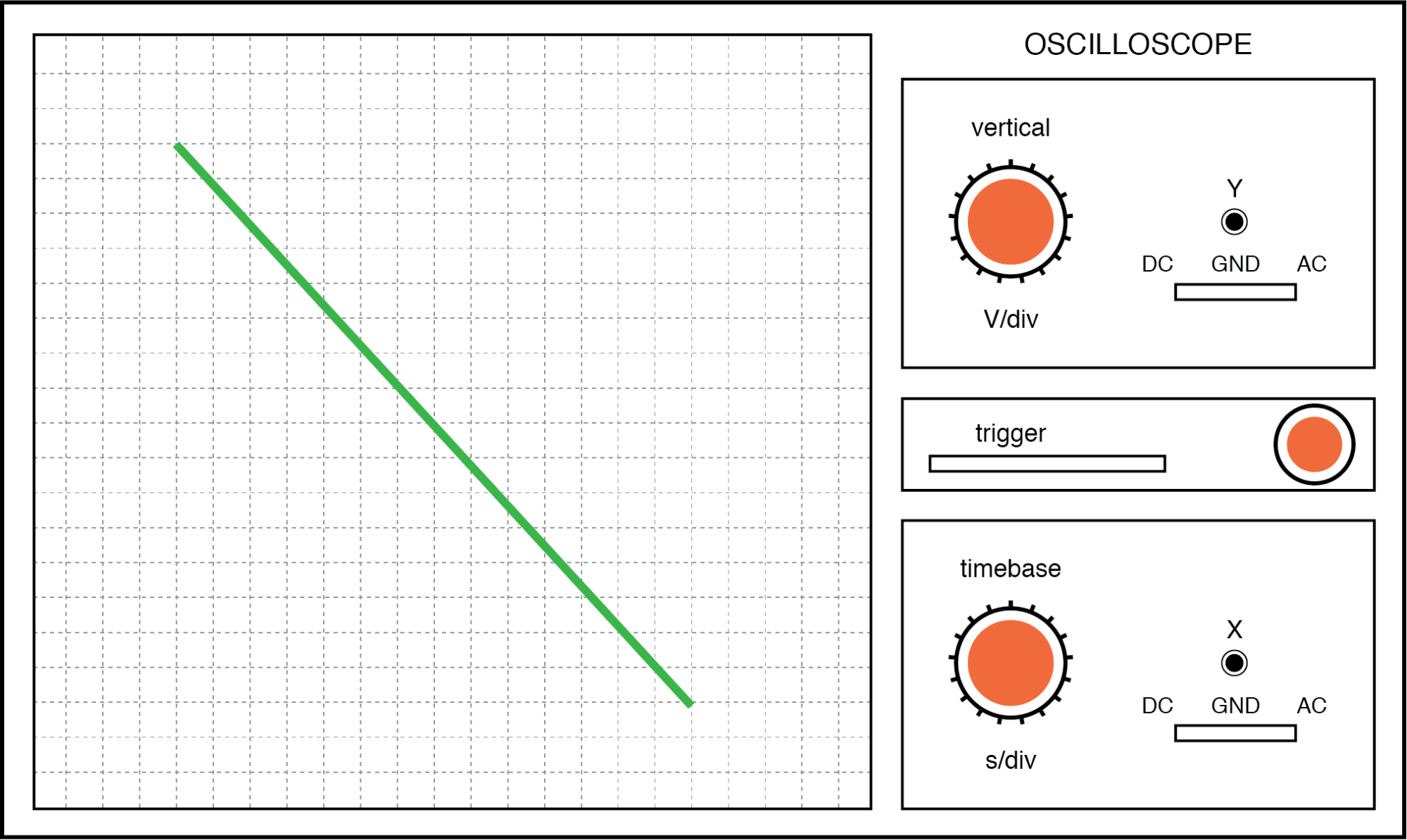
Lissajous-figuur:dezelfde frequentie, 180 graden faseverschuiving.

Wanneer we worden geconfronteerd met signaalfrequenties die niet hetzelfde zijn, worden de cijfers van Lissajous een stuk complexer. Bekijk de volgende voorbeelden en ze krijgen verticale/horizontale frequentieverhoudingen:

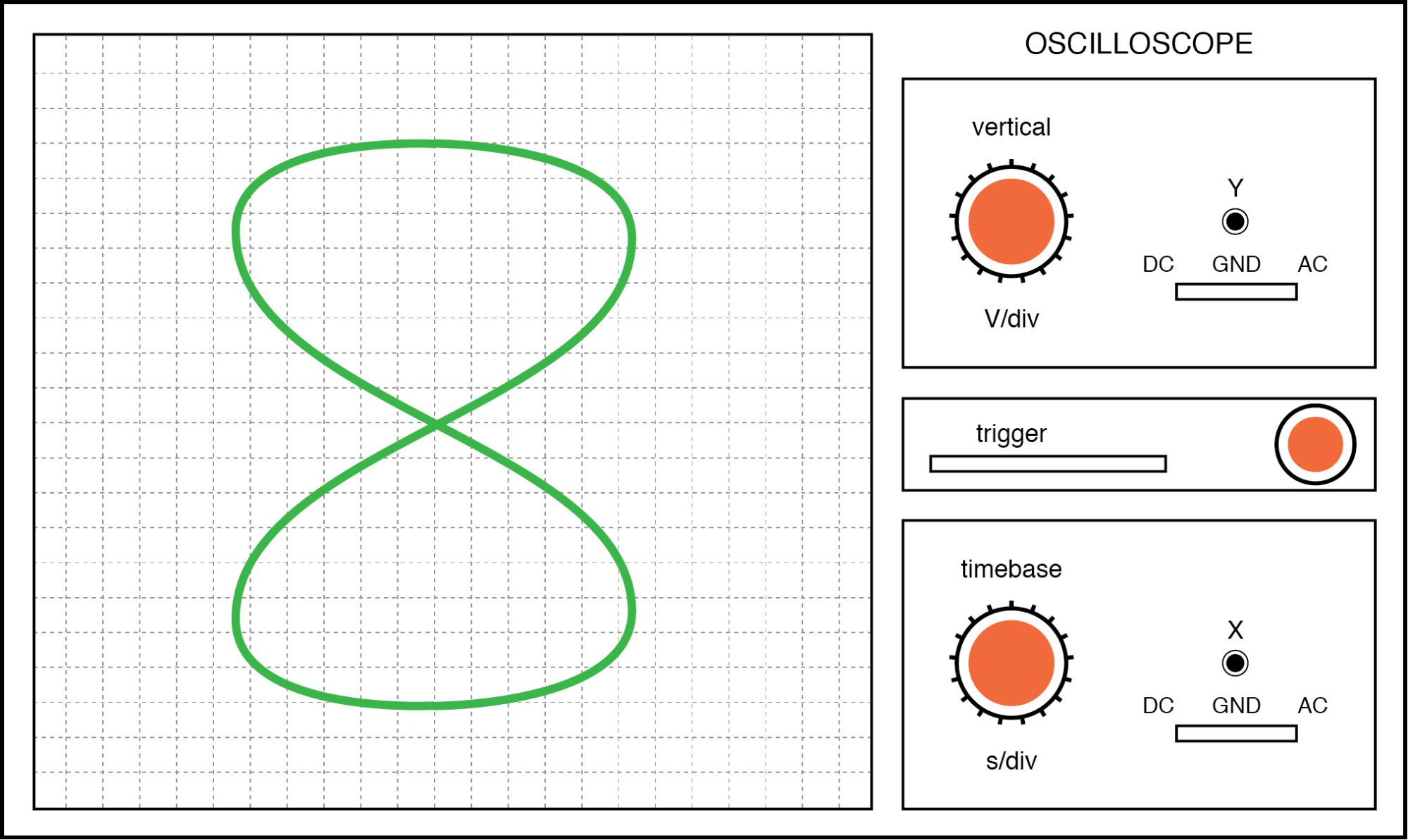
Lissajous-figuur:horizontale frequentie is twee keer zo groot als verticaal.

Hoe complexer de verhouding tussen horizontale en verticale frequenties, hoe complexer de Lissajous-figuur. Beschouw de volgende illustratie van een 3:1 frequentieverhouding tussen horizontaal en verticaal:

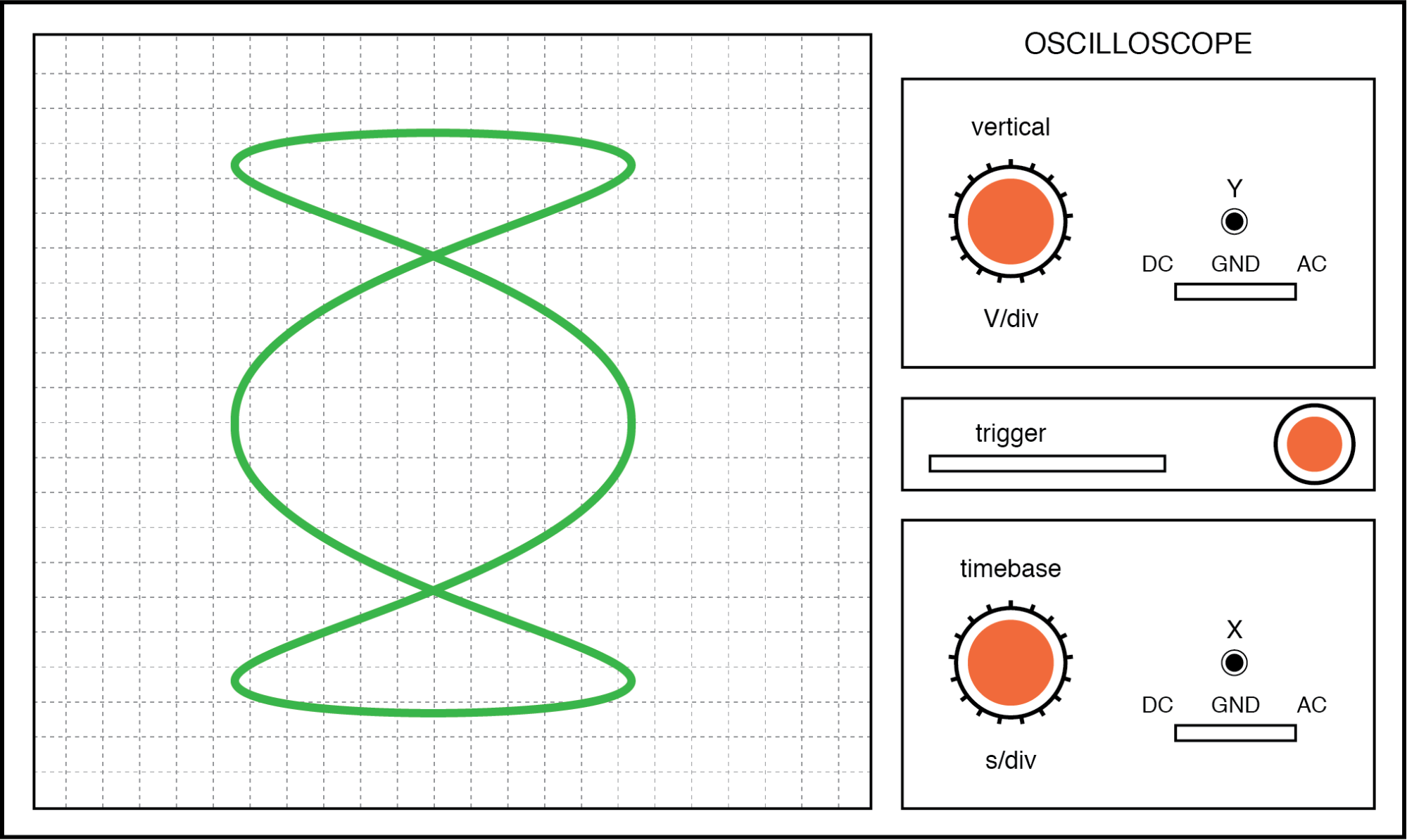
Lissajous-cijfer:horizontale frequentie is drie keer zo groot als verticaal.

. . . en een 3:2 frequentieverhouding (horizontaal =3, verticaal =2) in de onderstaande afbeelding.

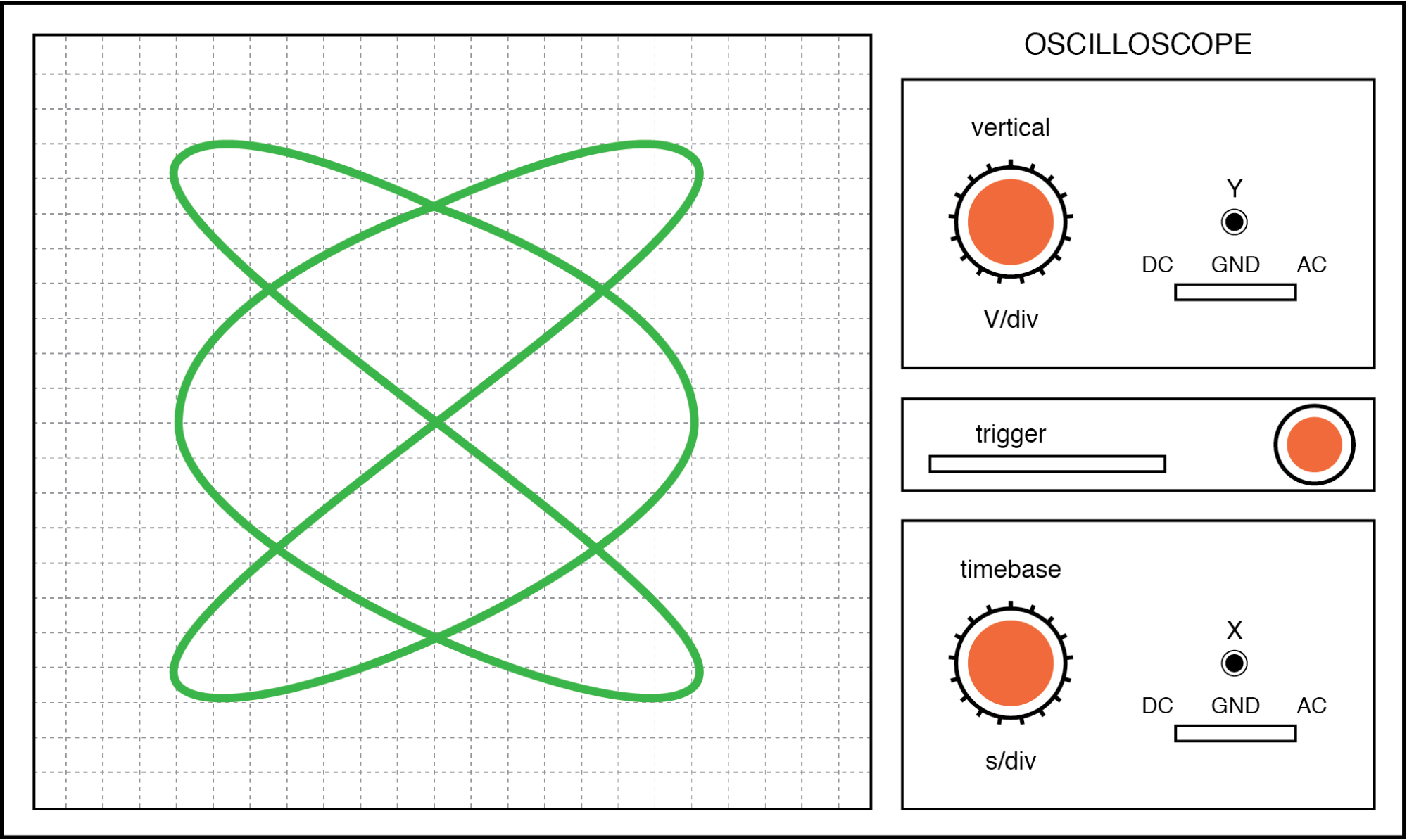
Lissajous-figuur:horizontale/verticale frequentieverhouding is 3:2.

In gevallen waarin de frequenties van de twee AC-signalen niet precies een eenvoudige verhouding van elkaar zijn (maar dichtbij), zal de Lissajous-figuur lijken te "bewegen", langzaam van richting veranderend terwijl de fasehoek tussen de twee golfvormen tussen 0 ° en 180°.

Als de twee frequenties zijn vergrendeld in een exacte integer-verhouding tussen elkaar, zal het Lissajous-cijfer stabiel zijn op het weergavescherm van de CRT.

De fysica van Lissajous-figuren beperkt hun bruikbaarheid als frequentievergelijkingstechniek tot gevallen waarin de frequentieverhoudingen eenvoudige gehele waarden zijn (1:1, 1:2, 1:3, 2:3, 3:4, enz.).

Ondanks deze beperking zijn Lissajous-cijfers een populair middel voor frequentievergelijking waar een toegankelijke frequentiestandaard (signaalgenerator) bestaat.

BEOORDELING:

• Sommige frequentiemeters werken volgens het principe van mechanische resonantie, waarbij de frequentie wordt aangegeven door relatieve oscillatie tussen een reeks uniek afgestemde "rieten" die op de gemeten frequentie worden geschud.
• Andere frequentiemeters gebruiken elektrische resonantiecircuits (meestal LC-tankcircuits) om de frequentie aan te geven. Een of beide componenten zijn instelbaar gemaakt, met een nauwkeurig gekalibreerde instelknop, en een gevoelige meter wordt afgelezen voor maximale spanning of stroom op het resonantiepunt.
• Frequentie kan op een vergelijkende manier worden gemeten, zoals het geval is bij het gebruik van een CRT om Lissajous-cijfers te genereren. Referentiefrequentiesignalen kunnen met een hoge mate van nauwkeurigheid worden gemaakt door oscillatorcircuits die kwartskristallen als resonantie-inrichtingen gebruiken. Voor ultraprecisie kunnen atoomkloksignaalstandaarden (gebaseerd op de resonantiefrequenties van individuele atomen) worden gebruikt.