Fast Fourier-transformaties berekenen op de LPC55S69 MCU

Dit artikel onderzoekt de Transform Engine, een ander onderdeel van de PowerQuad, waarmee de LPC55S69 MCU een Fast Fourier Transform (FFT) kan berekenen.

De LPC55S69-microcontroller van NXP bevat veel functies die hem geschikt maken voor een verscheidenheid aan toepassingen. De LPC55S69 MCU en zijn PowerQuad-eenheid bevatten unieke componenten - de Biquad en de Transform Engines - die worden gebruikt om verschillende taken uit te voeren, waardoor de belangrijkste CPU-kernen vrij blijven voor andere dingen.

Een vorig artikel, Digitale filtering begrijpen met ingebouwde microcontrollers, onderzocht verschillende veelgebruikte methoden voor het filteren en verwerken van gegevensmonsters in het tijdsdomein. Daarvoor gebruikte het de Biquad-engine van de PowerQuad-eenheid van de LPC55S69.

Dit artikel onderzoekt de Transform Engine, een ander onderdeel van de PowerQuad, waarmee de LPC55S69 MCU een Fast Fourier Transform (FFT) kan berekenen.

Discrete Fourier-transformaties begrijpen

Als het gaat om alledaagse metingen zoals lengtes en temperaturen, bestaat er een reeks hulpmiddelen om de grootte en temperatuur te bepalen van het specifieke ding dat wordt gemeten. Voor tijddomeinsignalen is de keuze van het meetinstrument misschien niet zo duidelijk. Beschouw het volgende signaalvoorbeeld in figuur 1.

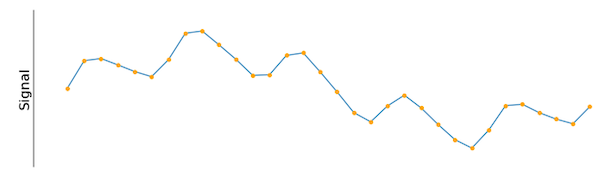
Figuur 1. Een ingangssignaal gesampled met een constant interval.

Hoe kan dit signaal worden gemeten, begrepen en beschreven? Mogelijke keuzes zijn de amplitude, de frequentie of meerdere waarden berekend met methoden uit de statistieken. Een manier om te beginnen is door het van belang zijnde signaal te meten tegen een bekende cosinusgolf, weergegeven in figuur 2.

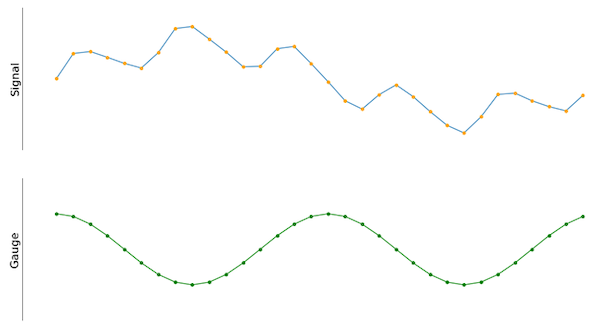
Figuur 2. Het ingangssignaal naast een cosinusmetersignaal. Beide hebben hetzelfde aantal monsters.

Omdat de amplitude en frequentie van de cosinusgolf gemakkelijk kunnen worden vastgesteld en dus geïdentificeerd, is het mogelijk om de cosinusgolf te vergelijken met het ingangssignaal. Indien correct gedaan, kwantificeert de resulterende waarde van het dot-product tussen het ingangssignaal en de cosinusgolf hoeveel het ingangssignaal correleert met de meter. Daarom is het redelijk om het ingangs- en meetsignaal te beschouwen als discrete ingangsarrays van dezelfde lengte, en het wordt gemakkelijk om het puntproduct te berekenen.

Het resultaat is een scalair en de grootte ervan is evenredig met hoe goed het ingangssignaal correleert met het cosinus-meetsignaal. De dot-productbewerking komt neer op vele vermenigvuldigings- en optelbewerkingen - dezelfde bewerking die wordt besproken in Digitale filtering begrijpen met ingebouwde microcontrollers.

Deze methode levert al snel goede resultaten op. Er is echter een specifiek geval dat niet werkt bij het toepassen van deze methode. Als het ingangssignaal een cosinusgolf is met dezelfde frequentie als de meter, maar waarvan de fase 90 graden verschoven is ten opzichte van de meter, zal de uitgang van de bovengenoemde methode nul zijn. Bij visuele inspectie blijkt dat er nog steeds een correlatie is tussen de meter en het ingangssignaal, maar er zijn details waar we rekening mee moeten houden.

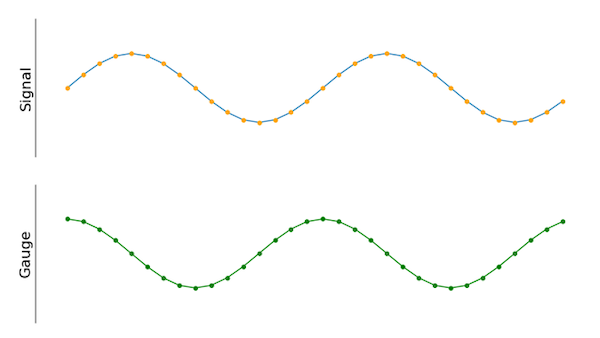
Figuur 3. Het nieuwe meetsignaal is 90 graden in fase verschoven ten opzichte van het oude.

Dit gedrag kan worden vergeleken met het meten van de "lengte" van een dunne strook papier. Wanneer u een liniaal gebruikt om de lengte van één zijde van de papierstrook te bepalen, kan het papier 10 inch lang en 2,5 cm breed zijn. Beide getallen zijn correct, maar de liniaal moest 90 graden worden gedraaid om beide metingen te verkrijgen. Beide nummers zijn technisch correct en we kunnen ze samen gebruiken om een ​​echte "grootte" (lengte en breedte) van ons stuk papier te krijgen. Om dit probleem met betrekking tot ons ingangssignaal op te lossen, kan een tweede meter worden gebruikt, zoals te zien is in figuur 4.

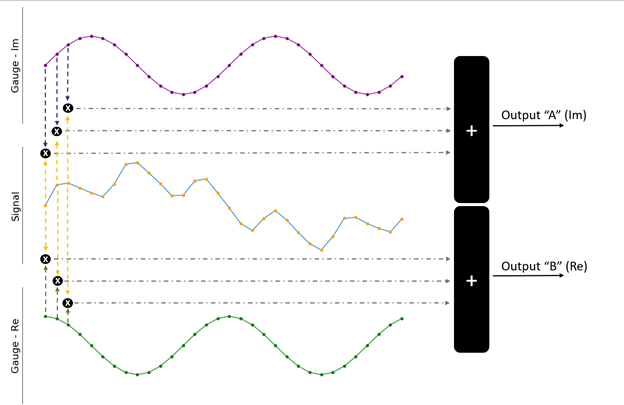
Figuur 4. Beide meetsignalen kunnen worden gebruikt om het ingangssignaal beter te kwantificeren.

Het enige verschil tussen de twee meters (weergegeven in paars en groen) is de faseverschuiving van 90 graden. In de vorige analogie is dit het equivalent van het draaien van de liniaal. Het dot-product wordt berekend tussen het ingangssignaal en elk van de meters om de uiteindelijke output te verkrijgen. Dit levert resultaten op in twee waarden A en B, die elk bevatten hoe goed de invoer correleert met een van de meters. Meestal worden ze beschouwd als een enkel complex getal:

output =B + i * A

De volgende stap is om het ingangssignaal te vergelijken met een reeks meters met verschillende frequenties (Figuur 5).

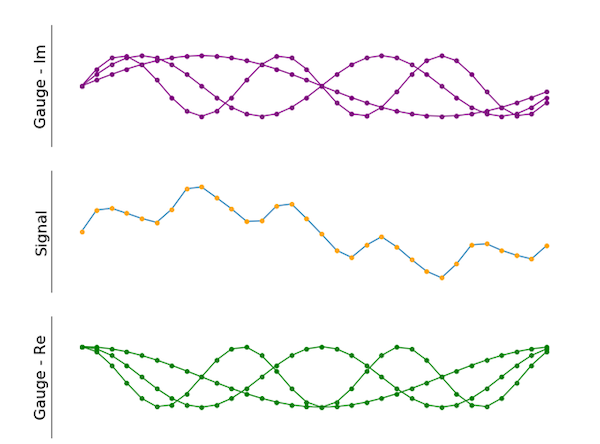
Figuur 5. Er kunnen ook meerdere meters worden toegepast. De groene zijn 90 graden verschoven ten opzichte van de paarse.

Zoals de afbeelding laat zien, bevat het eindresultaat een paar verschillende meters. Het denkbeeldige gedeelte (weergegeven in paars) is 90 graden in fase verschoven in vergelijking met de groene signalen (reële deel), net als in het bovenstaande voorbeeld van twee gauge. Er is geen limiet aan het aantal verschillende meters.

Het gebruik van deze techniek - de Discrete Fourier Transform (DFT) genoemd - levert het genereren van een spectrum van outputs op bij alle frequenties die van belang zijn voor een probleem. Het is mogelijk om de techniek als volgt wiskundig uit te drukken:

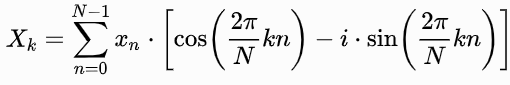
Vergelijking 1. De wiskundige beschrijving van de DFT.

Waarbij N het aantal samples in het ingangssignaal is en k de frequentie van de (co)sinusreferentiemeters.

Fast Fourier Transform (FFT)-beperkingen

De FFT is een numeriek efficiënte manier om de DFT te berekenen die minder vermenigvuldigings- en optelbewerkingen vereist in vergelijking met de hierboven besproken methode. Er zijn echter een paar beperkingen aan de invoer:

1. De lengte van de invoer moet een macht van twee zijn.
2. Willekeurige invoerlengtes en frequentie-afstanden in de uitvoer zijn niet toegestaan. De uitvoerbakken zijn verdeeld door de samplefrequentie van het ingangssignaal gedeeld door het aantal samples in de ingang. Als de invoer bijvoorbeeld een 256-punts signaal is dat is gesampled op 48 kHz, komen de uitvoerarrays overeen met frequenties op een onderlinge afstand van 187 Hz (48.000 gedeeld door 256).
3. Als de invoer uit reële getallen bestaat (bijvoorbeeld monsters verkregen van een ADC), is de uitvoer symmetrisch. Als de invoer bijvoorbeeld uit 64 steekproeven bestaat, zal het FFT-resultaat ook uit 64 complexe getallen bestaan. De tweede helft van de uitvoerarray bevat echter de complexe conjugaten van de eerste helft.

De PowerQuad FFT Engine gebruiken

De wiskunde achter DFT/FFT-bewerkingen kan worden uitgevoerd door eenvoudige bewerkingen voor vermenigvuldigen en optellen, wat ideaal is voor het uitbesteden van de wiskundige bewerkingen aan een speciale coprocessor, zoals de PowerQuad op de LPC55S69 MCU. Hierdoor zijn de belangrijkste CPU-kernen vrij om aan andere taken te werken.

Het gebruik van de PowerQuad FFT-engine is een eenvoudig proces en de officiële SDK wordt geleverd met voorbeeldprojecten die de coprocessing-functies demonstreren. Een voorbeeld in het bijzonder, powerquad_transform genaamd, demonstreert het FFT-berekeningsproces.

Het bestand powerquad_transform.c bevat verschillende functies die de verschillende FFT-engine-modi testen. Een daarvan is de functie PQ_RFFTFixed16Example. In dit voorbeeld wordt de PowerQuad geïnitialiseerd om 16-bits integer-gegevens te accepteren. Drijvende-kommagegevens moeten vooraf worden geconverteerd naar vaste-kommawaarden, aangezien de PowerQuad-transformatie-engine alleen gehele getallen ondersteunt.

FILTER_INPUT_LEN definieert het aantal invoermonsters. De uitvoerarray is twee keer zo lang omdat deze de echte en imaginaire delen van de resulterende waarden moet opslaan.

Figuur 6. Dit deel van de code definieert de testgegevens en de verwachte resultaten.

De laatste array bevat testgegevens om het resultaat te verifiëren. Merk op hoe de tweede helft van de array de complexe conjugaten bevat zoals hierboven vermeld. Verder zijn de conjugaten niet gelijk (bijvoorbeeld het paar 76,-50 en 77,49). Hoe dan ook, zodra de gegevens zijn geïnitialiseerd, wordt de volgende gegevensstructuur gebruikt om de PowerQuad te configureren:

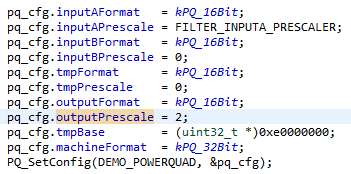
Figuur 7. Dit deel van het voorbeeldprogramma configureert en initialiseert de PowerQuad-eenheid.

Het is noodzakelijk om de invoer te verkleinen om te voorkomen dat het algoritme overloopt. Dit proces vindt plaats in de tweede regel in de afbeelding hierboven. FILTER_INPUTA_PRESCALER is ingesteld op vijf omdat er 32 (twee tot de macht van vijf) samples zijn. De pre-scaling is een andere hardwarefunctie van de PowerQuad en is waarschijnlijk de reden voor de onnauwkeurigheid die wordt waargenomen in de verwachte testresultaten.

Zodra alles is ingesteld, wordt de locatie van de invoer- en uitvoergebieden doorgegeven aan de PowerQuad-eenheid, wat gebeurt in de PQ_transformRFFT-functie. Deze methode stelt een paar configuratieregisters in en start de PowerQuad door naar het besturingsregister te schrijven. In dit voorbeeld wacht de CPU tot de PowerQuad klaar is. Wachten is niet altijd nodig en de PowerQuad kan berekeningen asynchroon uitvoeren terwijl de CPU andere taken uitvoert.

Gebruik de PowerQuad voor wiskundige bewerkingen

De PowerQuad is een coprocessor voor complexe wiskundige bewerkingen die beschikbaar is op verschillende apparaten van de LPC5500 MCU-serie. Het bevat een speciale engine voor het efficiënt berekenen van FFT's, die onafhankelijk van de belangrijkste CPU-kernen kan worden gedaan. De SDK voor de LPC55S69 MCU bevat voorbeelden van het instellen en gebruiken van de PowerQuad.

De communitypagina van NXP bevat uitgebreide informatie, discussies en artikelen over de LPC55S69 MCU.

Industrieartikelen zijn een vorm van inhoud waarmee branchepartners nuttig nieuws, berichten en technologie kunnen delen met lezers van All About Circuits op een manier waarop redactionele inhoud niet goed geschikt is. Alle brancheartikelen zijn onderworpen aan strikte redactionele richtlijnen met de bedoeling de lezers nuttig nieuws, technische expertise of verhalen te bieden. De standpunten en meningen in brancheartikelen zijn die van de partner en niet noodzakelijk die van All About Circuits of zijn schrijvers.