Conversie van decimale nummering

Omdat octale en hexadecimale nummeringssystemen basen hebben die veelvouden zijn van binair (grondtal 2), is de conversie heen en weer tussen hexadecimaal of octaal en binair heel eenvoudig.

Omdat we zo bekend zijn met het decimale systeem, is het converteren van binaire, octale of hexadecimale naar decimale vorm relatief eenvoudig (tel gewoon de producten van cijferwaarden en plaatsgewichten bij elkaar op).

De conversie van decimaal naar een van deze "vreemde" nummeringsystemen is echter een andere zaak.

Trial-and-Fit-methode

De methode die waarschijnlijk het meest logisch is, is de "trial-and-fit"-methode, waarbij u de binaire, octale of hexadecimale notatie probeert te "passen" op de gewenste waarde zoals weergegeven in decimale vorm.

Laten we bijvoorbeeld zeggen dat ik de decimale waarde van 87 in binaire vorm wilde weergeven. Laten we beginnen met het tekenen van een binair getalveld, compleet met plaatsgewichtswaarden:

Welnu, we weten dat we geen "1" bit in de plaats van 128 zullen hebben, want dat zou ons onmiddellijk een waarde geven die groter is dan 87.

Omdat het volgende gewicht aan de rechterkant (64) echter kleiner is dan 87, weten we dat we daar een "1" moeten hebben.

Als we de volgende plaats rechts ook een "1" zouden maken, zou onze totale waarde 64₁₀ zijn + 32₁₀ , of 96₁₀ . Dit is groter dan 87₁₀ , dus we weten dat dit bit een "0" moet zijn.

Als we de volgende plaatsbit van (16) gelijk maken aan "1", brengt dit onze totale waarde op 64₁₀ + 16₁₀ , of 80₁₀ , wat dichter bij onze gewenste waarde ligt (87₁₀ ) zonder deze te overschrijden:

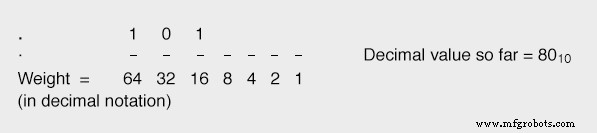
Door door te gaan in deze progressie, waarbij we elk bit met een lager gewicht instellen zoals we nodig hebben om onze gewenste totale waarde te bereiken zonder deze te overschrijden, zullen we uiteindelijk tot het juiste cijfer komen:

Trial-and-Fit-methode in octaal en hexadecimaal

Deze trial-and-fit-strategie werkt ook met octale en hexadecimale conversies. Laten we hetzelfde decimale getal nemen, 87₁₀ , en converteer het naar octale nummering:

Als we een cijfer van "1" in de plaats van 64 plaatsen, zouden we een totale waarde hebben van 64₁₀ (minder dan 87₁₀ ). Als we een cijfer van "2" in de plaats van 64 plaatsen, zouden we een totale waarde hebben van 128₁₀ (groter dan 87₁₀ ). Dit vertelt ons dat onze octale nummering moet beginnen met een "1" in de plaats van 64:

Nu moeten we experimenteren met cijferwaarden in de plaats van de 8 om te proberen een totale (decimale) waarde zo dicht mogelijk bij 87 te krijgen zonder deze te overschrijden. Als we de eerste paar coderingsopties proberen, krijgen we:

Een cijferwaarde van "3" op de plaats van de 8 zou ons boven het gewenste totaal van 87₁₀ brengen , dus "2" is het!

Als u tijdens het laatste gedeelte over octaal/binaire conversies goed oplet, zult u zich natuurlijk realiseren dat we de binaire representatie van (decimaal) 87₁₀ kunnen nemen. , waarvan we eerder hebben vastgesteld dat het 1010111₂ is , en converteer dat eenvoudig naar octaal om ons werk te controleren:

Kunnen we decimaal-naar-hexadecimaal op dezelfde manier converteren? Zeker, maar wie zou dat willen? Deze methode is eenvoudig te begrijpen, maar arbeidsintensief om uit te voeren.

Er is een andere manier om deze conversies uit te voeren, die in wezen hetzelfde is (wiskundig), maar gemakkelijker te bereiken.

Herhaaldedelingstechniek

Deze andere methode maakt gebruik van herhaalde delingscycli (met decimale notatie) om de decimale nummering op te splitsen in veelvouden van binaire, octale of hexadecimale plaats-gewichtswaarden.

In de eerste delingscyclus nemen we het oorspronkelijke decimale getal en delen dit door de basis van het nummeringssysteem waarnaar we converteren (binair =2 octaal =8, hex =16).

Vervolgens nemen we het gehele getal van het deelresultaat (quotiënt) en delen dit opnieuw door de basiswaarde, enzovoort, totdat we een quotiënt hebben dat kleiner is dan 1.

De binaire, octale of hexadecimale cijfers worden bepaald door de "resten" die overblijven bij elke deelstap. Laten we eens kijken hoe dit werkt voor binair, met het decimale voorbeeld van 87₁₀ :

De binaire bits worden samengesteld uit de resten van de opeenvolgende delingsstappen, beginnend met de LSB en doorgaand naar de MSB. In dit geval komen we uit op een binaire notatie van 1010111₂ .

Als we delen door 2, krijgen we altijd een quotiënt dat eindigt op ".0" of ".5", dat wil zeggen een rest van 0 of 1. Zoals eerder gezegd, zal deze herhalingsdelingstechniek voor conversie werken voor nummering andere systemen dan binair.

Als we opeenvolgende delingen zouden uitvoeren met een ander getal, zoals 8 voor conversie naar octaal, krijgen we noodzakelijkerwijs resten tussen 0 en 7. Laten we dit proberen met hetzelfde decimale getal, 87₁₀ :

We kunnen een vergelijkbare techniek ook gebruiken voor het converteren van nummeringsystemen die omgaan met hoeveelheden kleiner dan 1.

Om een ​​decimaal getal kleiner dan 1 om te zetten in binair, octaal of hexadecimaal, gebruiken we herhaalde vermenigvuldiging, waarbij we het gehele deel van het product in elke stap nemen als het volgende cijfer van ons geconverteerde getal.

Laten we het decimale getal 0.8125₁₀ . gebruiken bijvoorbeeld converteren naar binair:

Net als bij het herhaalde delingsproces voor gehele getallen, geeft elke stap ons het volgende cijfer (of bit) verder weg van het "punt".

Met integer (delen) werkten we van de LSB naar de MSB (van rechts naar links), maar met herhaalde vermenigvuldiging werkten we van links naar rechts.

Om een ​​decimaal getal groter dan 1 met een <1 component te converteren, moeten we beide . gebruiken technieken, één voor één. Neem het decimale voorbeeld van 54.40625₁₀ , converteren naar binair:

GERELATEERDE WERKBLAD:

• Werkblad Nummeringsystemen