Kwantumfysica

“Ik denk dat het veilig is om te zeggen dat niemand kwantum begrijpt mechanica.” —Natuurkundige Richard P. Feynman

Om te zeggen dat de uitvinding van halfgeleiderapparaten een revolutie was, zou niet overdreven zijn. Dit was niet alleen een indrukwekkende technologische prestatie, maar het maakte ook de weg vrij voor ontwikkelingen die de moderne samenleving onuitwisbaar zouden veranderen. Halfgeleiderapparatuur maakte geminiaturiseerde elektronica mogelijk, waaronder computers, bepaalde soorten medische diagnose- en behandelingsapparatuur en populaire telecommunicatieapparatuur, om maar een paar toepassingen van deze technologie te noemen.

Achter deze revolutie in technologie staat een nog grotere revolutie in de algemene wetenschap:het gebied van kwantumfysica . Zonder deze sprong in het begrijpen van de natuurlijke wereld, zou de ontwikkeling van halfgeleiderapparaten (en meer geavanceerde elektronische apparaten die nog in ontwikkeling zijn) nooit mogelijk zijn geweest. Kwantumfysica is een ongelooflijk gecompliceerd domein van de wetenschap. Dit hoofdstuk is slechts een beknopt overzicht. Als wetenschappers van het kaliber van Feynman zeggen dat "niemand [het] begrijpt", kun je er zeker van zijn dat het een complex onderwerp is. Zonder een basiskennis van de kwantumfysica, of op zijn minst een begrip van de wetenschappelijke ontdekkingen die tot de formulering hebben geleid, is het echter onmogelijk om te begrijpen hoe en waarom elektronische halfgeleiderapparaten werken. De meeste inleidende elektronica-handboeken die ik heb gelezen, proberen halfgeleiders uit te leggen in termen van 'klassieke' fysica, wat resulteert in meer verwarring dan begrip.

Atoom

Velen van ons hebben diagrammen gezien van atomen die er ongeveer zo uitzien als de onderstaande afbeelding.

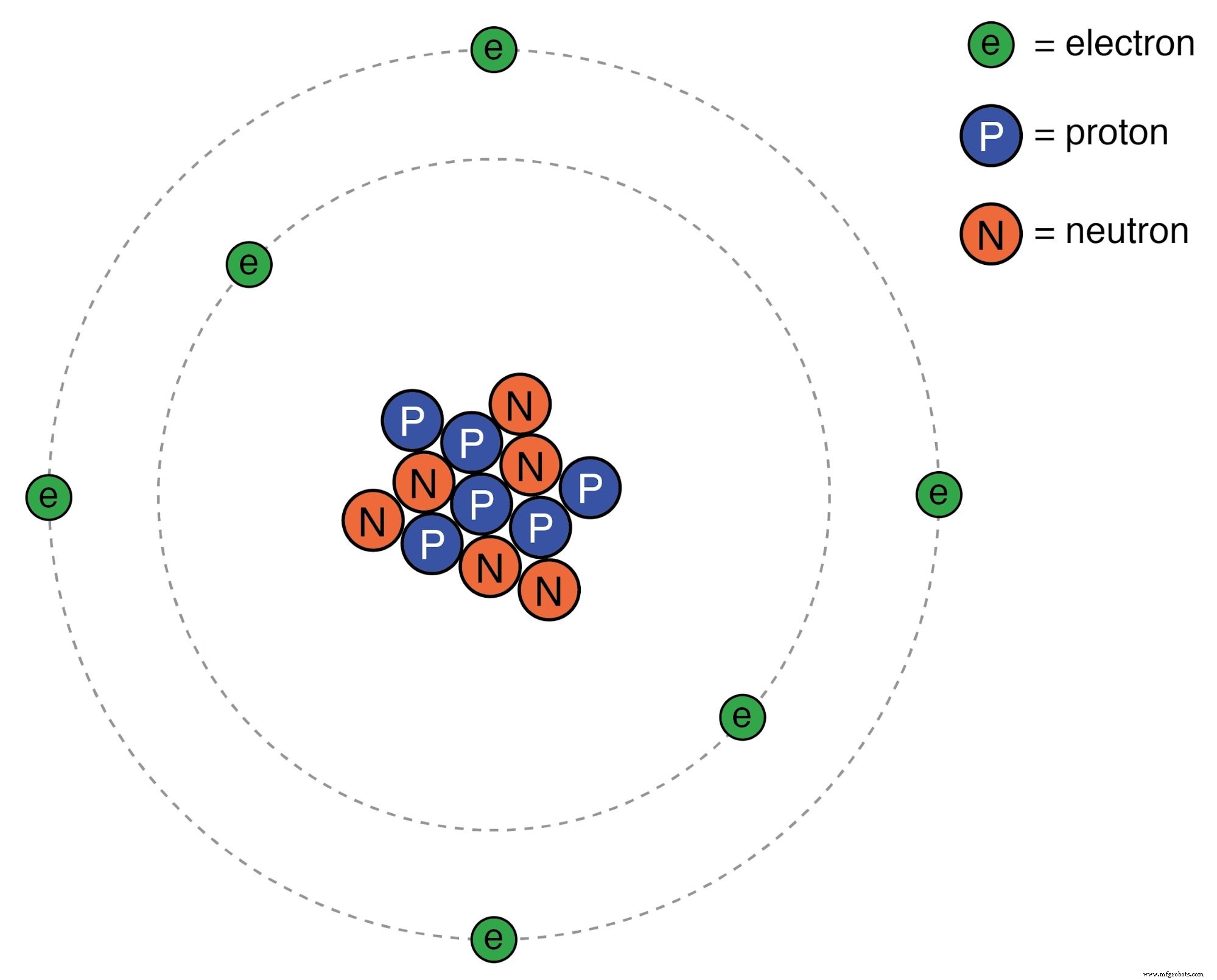
Rutherford-atoom:negatieve elektronen draaien om een ​​kleine positieve kern.

Kleine deeltjes materie genaamd protonen en neutronen vormen het centrum van het atoom; elektronen draaien als planeten rond een ster. De kern draagt ​​een positieve elektrische lading vanwege de aanwezigheid van protonen (de neutronen hebben helemaal geen elektrische lading), terwijl de negatieve lading van het atoom zich in de ronddraaiende elektronen bevindt. De negatieve elektronen worden aangetrokken door de positieve protonen, net zoals planeten door de zwaartekracht worden aangetrokken door de zon, maar de banen zijn stabiel vanwege de beweging van de elektronen. We hebben dit populaire model van het atoom te danken aan het werk van Ernest Rutherford, die rond het jaar 1911 experimenteel vaststelde dat de positieve ladingen van atomen waren geconcentreerd in een kleine, dichte kern in plaats van gelijkmatig over de diameter te worden verdeeld, zoals werd voorgesteld door een eerdere onderzoeker , JJ Thompson.

Rutherfords verstrooiing

Het verstrooiingsexperiment van Rutherford omvat het bombarderen van een dunne goudfolie met positief geladen alfadeeltjes, zoals in de onderstaande afbeelding. Jonge afgestudeerde studenten H. Geiger en E. Marsden ondervonden onverwachte resultaten. Een paar alfadeeltjes werden onder grote hoeken afgebogen. Een paar alfadeeltjes werden terugverstrooid en deinsden terug met bijna 180 ^o . De meeste deeltjes gingen onafgebogen door de goudfolie, wat aangeeft dat de folie grotendeels lege ruimte was. Het feit dat een paar alfadeeltjes grote doorbuigingen ondervonden, duidde op de aanwezigheid van een minuscule positief geladen kern.

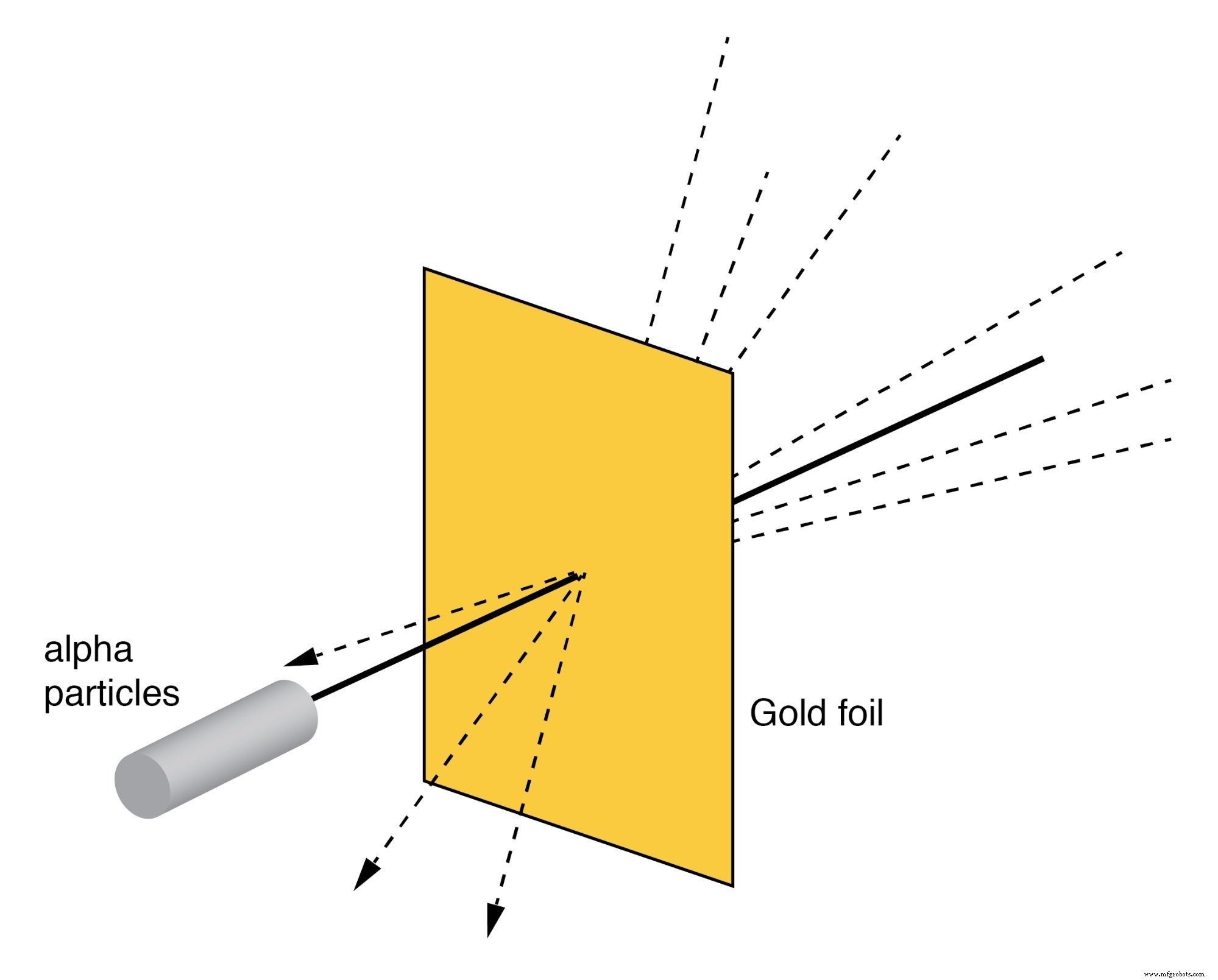
Rutherford-verstrooiing:een bundel alfadeeltjes wordt verstrooid door een dunne gouden folie.

Hoewel het atomaire model van Rutherford de experimentele gegevens beter weergaf dan dat van Thompson, was het nog steeds niet perfect. Er werden verdere pogingen ondernomen om de atomaire structuur te definiëren, en deze inspanningen hielpen de weg vrij te maken voor de bizarre ontdekkingen van de kwantumfysica. Tegenwoordig is ons begrip van het atoom een ​​stuk complexer. Desalniettemin, ondanks de revolutie van de kwantumfysica en haar bijdrage aan ons begrip van de atomaire structuur, heeft Rutherfords zonnestelselbeeld van het atoom zich in zo'n mate in het populaire bewustzijn ingebed dat het in sommige studiegebieden blijft bestaan, zelfs als het ongepast is.

Beschouw deze korte beschrijving van elektronen in een atoom, ontleend aan een populair elektronicaboek:

Negatieve elektronen in een baan om de aarde worden daarom aangetrokken naar de positieve kern, wat ons leidt tot de vraag waarom de elektronen niet in de atoomkern vliegen. Het antwoord is dat de in een baan om de aarde draaiende elektronen in hun stabiele baan blijven vanwege twee gelijke maar tegengestelde krachten. De uitwendige centrifugale kracht die door de baan op de elektronen wordt uitgeoefend, werkt de aantrekkende binnenwaartse kracht (centripetaal) tegen die de elektronen naar de kern probeert te trekken vanwege de ongelijke ladingen.

In overeenstemming met het Rutherford-model werpt deze auteur de elektronen als vaste brokken materie die zich in cirkelvormige banen bevinden, waarbij hun innerlijke aantrekkingskracht op de tegengesteld geladen kern in evenwicht wordt gehouden door hun beweging. De verwijzing naar "centrifugale kracht" is technisch onjuist (zelfs voor planeten die in een baan rond de aarde draaien), maar wordt gemakkelijk vergeven vanwege de populaire acceptatie:in werkelijkheid bestaat er niet zoiets als een kracht die een voortstuwt in een baan rond het lichaam weg vanuit het middelpunt van de baan. Het lijkt zo omdat de traagheid van een lichaam de neiging heeft om het in een rechte lijn te laten reizen, en aangezien een baan een constante afwijking (versnelling) is van rechtlijnig reizen, is er een constante traagheidsoppositie tegen welke kracht dan ook die het lichaam naar de baan trekt centrum (centripetaal), of het nu zwaartekracht, elektrostatische aantrekking of zelfs de spanning van een mechanische verbinding is.

Het echte probleem met deze verklaring is echter het idee dat elektronen in de eerste plaats in cirkelvormige banen reizen. Het is een verifieerbaar feit dat versnellende elektrische ladingen elektromagnetische straling uitzenden, en dit feit was zelfs in de tijd van Rutherford bekend. Omdat beweging in een baan een vorm van versnelling is (het ronddraaiende object in constante versnelling weg van de normale, rechtlijnige beweging), zouden elektronen in een baan om de aarde straling moeten afstoten zoals modder van een draaiende band. Elektronen versnelden rond cirkelvormige paden in deeltjesversnellers genaamd synchrotrons waarvan bekend is dat ze dit doen, en het resultaat wordt synchrotronstraling genoemd . Als elektronen op deze manier energie zouden verliezen, zouden hun banen uiteindelijk vervallen, wat zou resulteren in botsingen met de positief geladen kern. Toch gebeurt dit normaal gesproken niet binnen atomen. De "banen" van elektronen zijn inderdaad opmerkelijk stabiel onder een breed scala aan omstandigheden.

Opgewonden Atomen

Bovendien toonden experimenten met "opgewonden" atomen aan dat elektromagnetische energie die door een atoom wordt uitgezonden, alleen voorkomt bij bepaalde, welomlijnde frequenties. Van atomen die 'opgewonden' worden door invloeden van buitenaf, zoals licht, is bekend dat ze die energie absorberen en teruggeven als elektromagnetische golven met specifieke frequenties, zoals een stemvork die op een vaste toon klinkt, ongeacht hoe erop wordt geslagen. Wanneer het licht dat door een aangeslagen atoom wordt uitgezonden door een prisma in zijn samenstellende frequenties (kleuren) wordt verdeeld, verschijnen er duidelijke kleurlijnen in het spectrum, waarbij het patroon van spectraallijnen uniek is voor dat element. Dit fenomeen wordt vaak gebruikt om atomaire elementen te identificeren en zelfs de verhoudingen van elk element in een verbinding of chemisch mengsel te meten. Volgens het atomaire model van het zonnestelsel van Rutherford (waarbij elektronen worden beschouwd als brokken materie die vrij in een baan rond elke straal kunnen draaien) en de wetten van de klassieke fysica, zouden aangeslagen atomen energie moeten teruggeven over een vrijwel onbeperkt bereik van frequenties in plaats van een select aantal. Met andere woorden, als het model van Rutherford correct zou zijn, zou er geen "stemvork" -effect zijn en zou het lichtspectrum dat door een atoom wordt uitgezonden, verschijnen als een doorlopende band van kleuren in plaats van als een paar duidelijke lijnen.

BohrModel

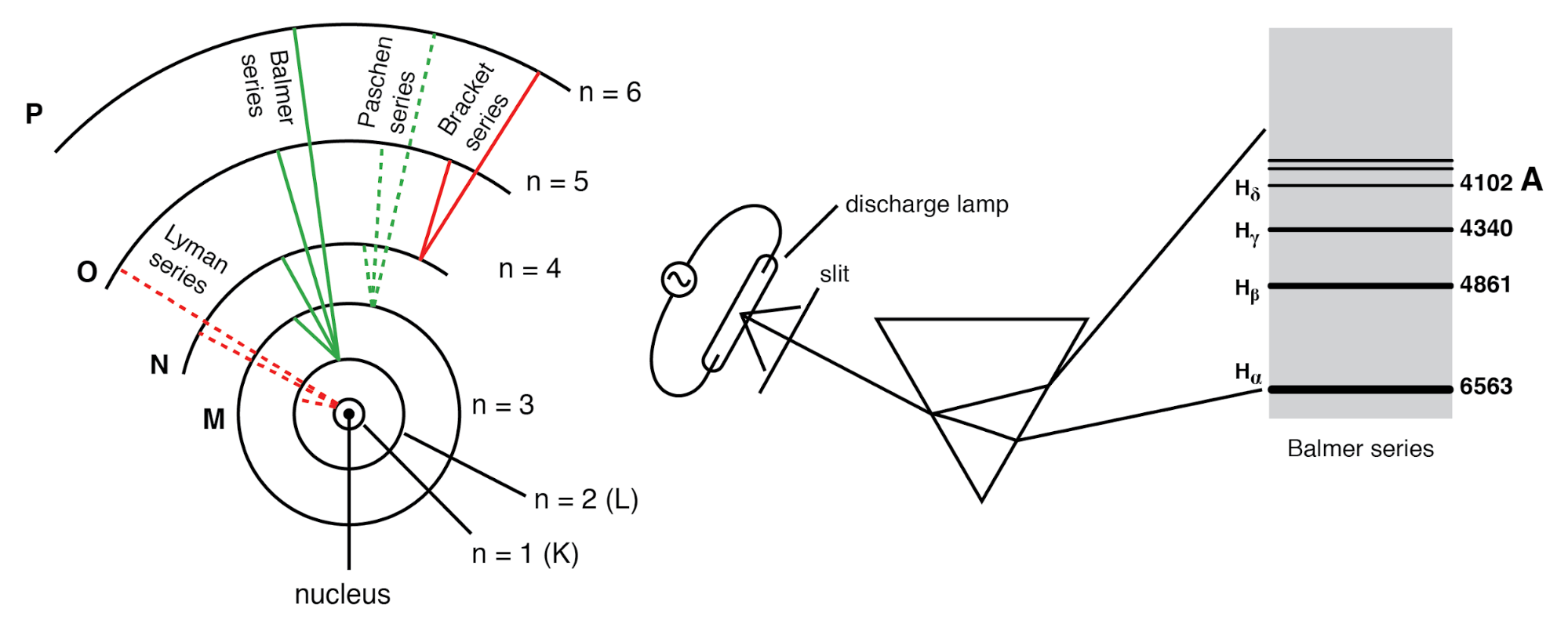
Bohr-waterstofatoom (met banen op schaal getekend) laat alleen elektronen toe om discrete orbitalen te bewonen. Elektronen die van n=3,4,5 of 6 naar n=2 vallen, zijn verantwoordelijk voor de reeksen spectraallijnen van Balmer.

Een baanbrekende onderzoeker genaamd Niels Bohr probeerde het model van Rutherford te verbeteren nadat hij in 1912 enkele maanden in het laboratorium van Rutherford had gestudeerd. In een poging de bevindingen van andere natuurkundigen (met name Max Planck en Albert Einstein) te harmoniseren, suggereerde Bohr dat elk elektron een bepaalde, specifieke hoeveelheid energie hadden, en dat hun banen werden gekwantiseerd zodanig dat elk bepaalde plaatsen rond de kern kan innemen, zoals knikkers die in cirkelvormige sporen rond de kern zijn vastgezet in plaats van de vrijlopende satellieten waarvan vroeger werd gedacht dat ze waren. (Figuur hierboven) Uit eerbied voor de wetten van elektromagnetisme en versnellende ladingen, zinspeelde Bohr op deze "banen" als stationaire toestanden om te ontsnappen aan de implicatie dat ze in beweging waren. Hoewel Bohrs ambitieuze poging om de structuur van het atoom opnieuw in te kaderen in termen die dichter bij de experimentele resultaten kwamen, een mijlpaal in de natuurkunde was, was het niet compleet. Zijn wiskundige analyse leverde betere voorspellingen van experimentele gebeurtenissen op dan analyses die tot eerdere modellen behoorden, maar er waren nog steeds enkele onbeantwoorde vragen over het waarom elektronen zouden zich op zulke vreemde manieren moeten gedragen. De bewering dat elektronen in stationaire, gekwantiseerde toestanden rond de kern bestonden, gaf een betere verklaring voor experimentele gegevens dan het model van Rutherford, maar hij had geen idee wat elektronen zou dwingen om die specifieke toestanden te manifesteren. Het antwoord op die vraag moest ongeveer tien jaar later komen van een andere natuurkundige, Louis de Broglie.

De Broglie-hypothese

De Broglie stelde voor dat elektronen, als fotonen (lichtdeeltjes) zowel deeltjesachtige als golfachtige eigenschappen vertonen. Voortbouwend op dit voorstel suggereerde hij dat een analyse van elektronen in een baan vanuit een golfperspectief in plaats van een deeltjesperspectief hun gekwantiseerde aard beter zou kunnen begrijpen. Er werd inderdaad een nieuwe doorbraak in begrip bereikt.

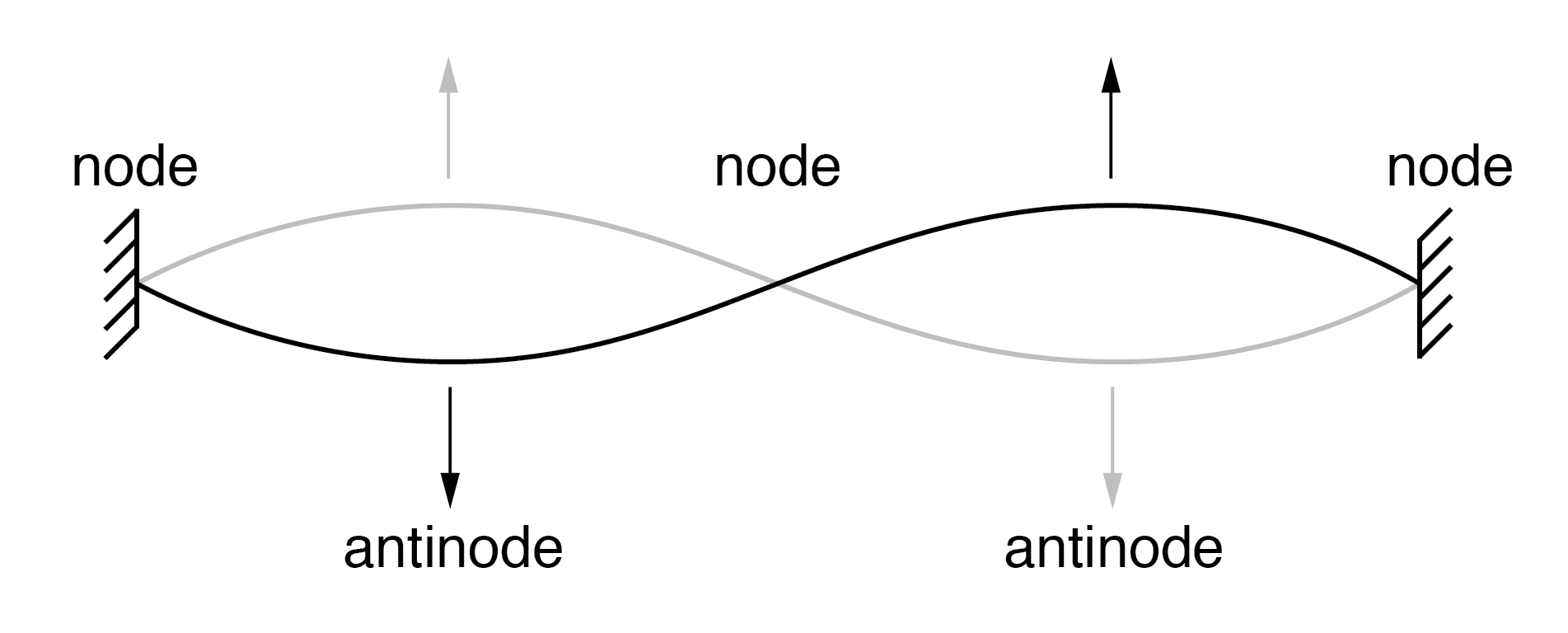
Snaar die op resonantiefrequentie trilt tussen twee vaste punten vormt staande golf .

Het atoom volgens de Broglie bestond uit elektronen die bestonden als staande golven , een fenomeen dat natuurkundigen in verschillende vormen goed kennen. Zoals de getokkelde snaar van een muziekinstrument (Figuur hierboven) die trilt met een resonantiefrequentie, met "knopen" en "antinodes" op stabiele posities langs de lengte. De Broglie zag elektronen rond atomen staan ​​als golven die rond een cirkel waren gebogen, zoals in het onderstaande figuur.

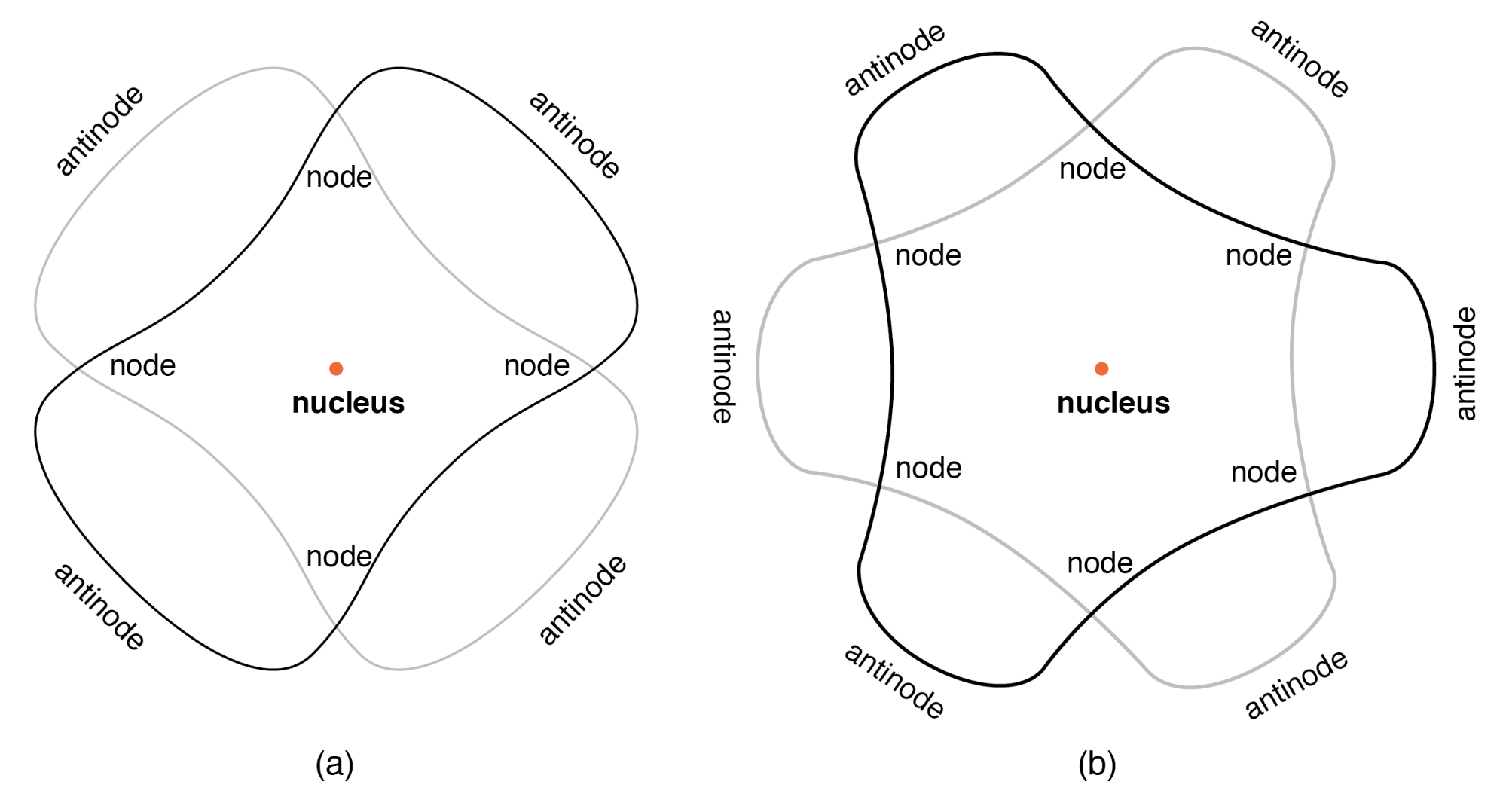
"Baan" elektron als staande golf rond de kern, (a) twee cycli per baan, (b) drie cycli per baan.

Elektronen konden alleen in bepaalde, duidelijke "banen" rond de kern bestaan, omdat dat de enige afstanden waren waar de golfuiteinden overeen zouden komen. In elke andere straal zou de golf zichzelf destructief moeten verstoren en dus ophouden te bestaan. De Broglie's hypothese gaf zowel wiskundige ondersteuning als een handige fysieke analogie om de gekwantiseerde toestanden van elektronen binnen een atoom te verklaren, maar zijn atoommodel was nog steeds onvolledig. Maar binnen een paar jaar bouwden natuurkundigen Werner Heisenberg en Erwin Schrodinger, onafhankelijk van elkaar, voort op De Broglie's concept van een materie-golf-dualiteit om meer wiskundig rigoureuze modellen van subatomaire deeltjes te creëren.

Kwantummechanica

Deze theoretische vooruitgang van het primitieve staande golfmodel van De Broglie naar de matrix van Heisenberg en de differentiaalvergelijkingsmodellen van Schrödinger kreeg de naam kwantummechanica , en het introduceerde een nogal schokkende eigenschap in de wereld van subatomaire deeltjes:de eigenschap van waarschijnlijkheid of onzekerheid. Volgens de nieuwe kwantumtheorie was het onmogelijk om de exacte positie te bepalen en exacte impuls van een deeltje op hetzelfde moment. De populaire verklaring van dit "onzekerheidsprincipe" was dat het een meetfout was (dwz door te proberen de positie van een elektron nauwkeurig te meten, interfereert u met zijn momentum en kunt u dus niet weten wat het was voordat de positiemeting werd uitgevoerd, en vice versa. omgekeerd). De verrassende implicatie van de kwantummechanica is dat deeltjes eigenlijk geen precieze posities hebben en momenta, maar balanceer de twee grootheden op een zodanige manier dat hun gecombineerde onzekerheden nooit onder een bepaalde minimumwaarde afnemen.

Deze vorm van "onzekerheids"-relatie bestaat op andere gebieden dan de kwantummechanica. Zoals besproken in het hoofdstuk "Mixed-Frequency AC Signals" in deel II van deze boekenreeks, is er een wederzijds uitsluitende relatie tussen de zekerheid van de tijddomeingegevens van een golfvorm en de frequentiedomeingegevens. In eenvoudige bewoordingen, hoe nauwkeuriger we de samenstellende frequentie(s) kennen, hoe minder precies we de amplitude ervan in de tijd kennen, en vice versa. Om mezelf te citeren:

Een golfvorm van oneindige duur (oneindig aantal cycli) kan met absolute precisie worden geanalyseerd, maar hoe minder cycli beschikbaar zijn voor de computer voor analyse, hoe minder nauwkeurig de analyse. . . Hoe minder keer een golf cycli, hoe minder zeker de frequentie is. Om dit concept tot zijn logische uiterste door te voeren, heeft een korte puls - een golfvorm die niet eens een cyclus voltooit - eigenlijk geen frequentie, maar fungeert eerder als een oneindig bereik van frequenties. Dit principe geldt voor alle op golven gebaseerde verschijnselen, niet alleen voor wisselspanningen en -stromen.

Om de amplitude van een variërend signaal nauwkeurig te bepalen, moeten we het over een zeer korte tijdspanne bemonsteren. Dit beperkt echter ons zicht op de frequentie van de golf. Omgekeerd, om de frequentie van een golf met grote precisie te bepalen, moeten we deze gedurende vele cycli bemonsteren, wat betekent dat we op elk moment het zicht op de amplitude verliezen. We kunnen dus niet tegelijkertijd de momentane amplitude en de algehele frequentie van een golf met onbeperkte precisie kennen. Vreemder nog, deze onzekerheid is veel meer dan de onnauwkeurigheid van de waarnemer; het ligt in de aard van de golf. Het is niet alsof het, gegeven de juiste technologie, mogelijk zou zijn om nauwkeurige metingen te verkrijgen van beide momentane amplitude en frequentie tegelijk. Letterlijk kan een golf niet tegelijkertijd een precieze, onmiddellijke amplitude en een precieze frequentie hebben.

De minimale onzekerheid van de positie en het momentum van een deeltje, uitgedrukt door Heisenberg en Schrödinger, heeft niets te maken met beperking in meting; het is eerder een intrinsieke eigenschap van de materie-golf dualiteit van het deeltje. Elektronen bestaan ​​daarom niet echt in hun "banen" als nauwkeurig gedefinieerde stukjes materie, of zelfs als nauwkeurig gedefinieerde golfvormen, maar eerder als "wolken" - de technische term is golffunctie -van waarschijnlijkheidsverdeling, alsof elk elektron is "verspreid" of "uitgesmeerd" over een reeks posities en momenten.

Deze radicale kijk op elektronen als onnauwkeurige wolken lijkt in eerste instantie in tegenspraak met het oorspronkelijke principe van gekwantiseerde elektronentoestanden:dat elektronen bestaan ​​in discrete, gedefinieerde "banen" rond atoomkernen. Het was tenslotte deze ontdekking die leidde tot de vorming van de kwantumtheorie om het te verklaren. Hoe vreemd lijkt het dat een theorie die is ontwikkeld om het discrete gedrag van elektronen te verklaren, uiteindelijk verklaart dat elektronen bestaan ​​als "wolken" in plaats van als afzonderlijke stukjes materie. Het gekwantiseerde gedrag van elektronen hangt echter niet af van elektronen met duidelijke positie- en momentumwaarden, maar eerder van andere eigenschappen die kwantumgetallen worden genoemd. . In wezen ziet de kwantummechanica af van algemeen aanvaarde noties van absolute positie en absoluut momentum, en vervangt ze door absolute noties van een soort die geen analogie hebben met de algemene ervaring.

Vier kwantumgetallen

Hoewel bekend is dat elektronen bestaan ​​in etherische, "wolkachtige" vormen van gedistribueerde waarschijnlijkheid in plaats van als afzonderlijke brokken materie, hebben die "wolken" andere kenmerken die zijn discreet. Elk elektron in een atoom kan worden beschreven met vier numerieke maten (de eerder genoemde kwantumgetallen ), genaamd de Principaal , Angular Momentum , Magnetisch , en Spin nummers. Het volgende is een samenvatting van de betekenissen van elk van deze getallen:

1. Hoofdkwantumnummer

Hoofdkwantumnummer: Gesymboliseerd door de letter n , dit nummer beschrijft de schaal waarin een elektron zich bevindt. Een elektronenschil is een ruimtegebied rond de atoomkern waar elektronen mogen bestaan, wat overeenkomt met de stabiele staande golfpatronen van de Broglie en Bohr. Elektronen kunnen van schaal naar schaal "springen", maar kunnen niet bestaan ​​tussen de schelpengebieden. Het hoofdkwantumgetal moet een positief geheel getal zijn (een geheel getal, groter dan of gelijk aan 1). Met andere woorden, het principe-kwantumgetal voor een elektron kan niet 1/2 of -3 zijn. Deze gehele waarden zijn niet willekeurig tot stand gekomen, maar eerder door experimenteel bewijs van lichtspectra:de verschillende frequenties (kleuren) van het licht dat wordt uitgezonden door aangeslagen waterstofatomen volgen een reeks die wiskundig afhankelijk is van specifieke, gehele waarden, zoals geïllustreerd in de vorige afbeelding.

Elke schil heeft de capaciteit om meerdere elektronen vast te houden. Een analogie voor elektronenschillen zijn de concentrische rijen stoelen van een amfitheater. Net zoals een persoon die in een amfitheater zit, een rij moet kiezen om in te zitten (men kan niet tussen rijen), moeten elektronen een bepaalde schil "kiezen" om in te "zitten". Net als in amfitheaterrijen bevatten de buitenste schillen meer elektronen dan de binnenste schillen. Ook hebben elektronen de neiging om de laagst beschikbare schil te zoeken, zoals mensen in een amfitheater de dichtstbijzijnde stoel bij het middelpunt zoeken. Hoe hoger het schaalnummer, hoe groter de energie van de elektronen erin.

Het maximale aantal elektronen dat een schil kan bevatten, wordt beschreven door de vergelijking 2n ² , waarbij "n" het belangrijkste kwantumgetal is. De eerste schil (n=1) kan dus 2 elektronen bevatten; de tweede schil (n=2) 8 elektronen, en de derde schil (n=3) 18 elektronen. (Figuur hieronder)

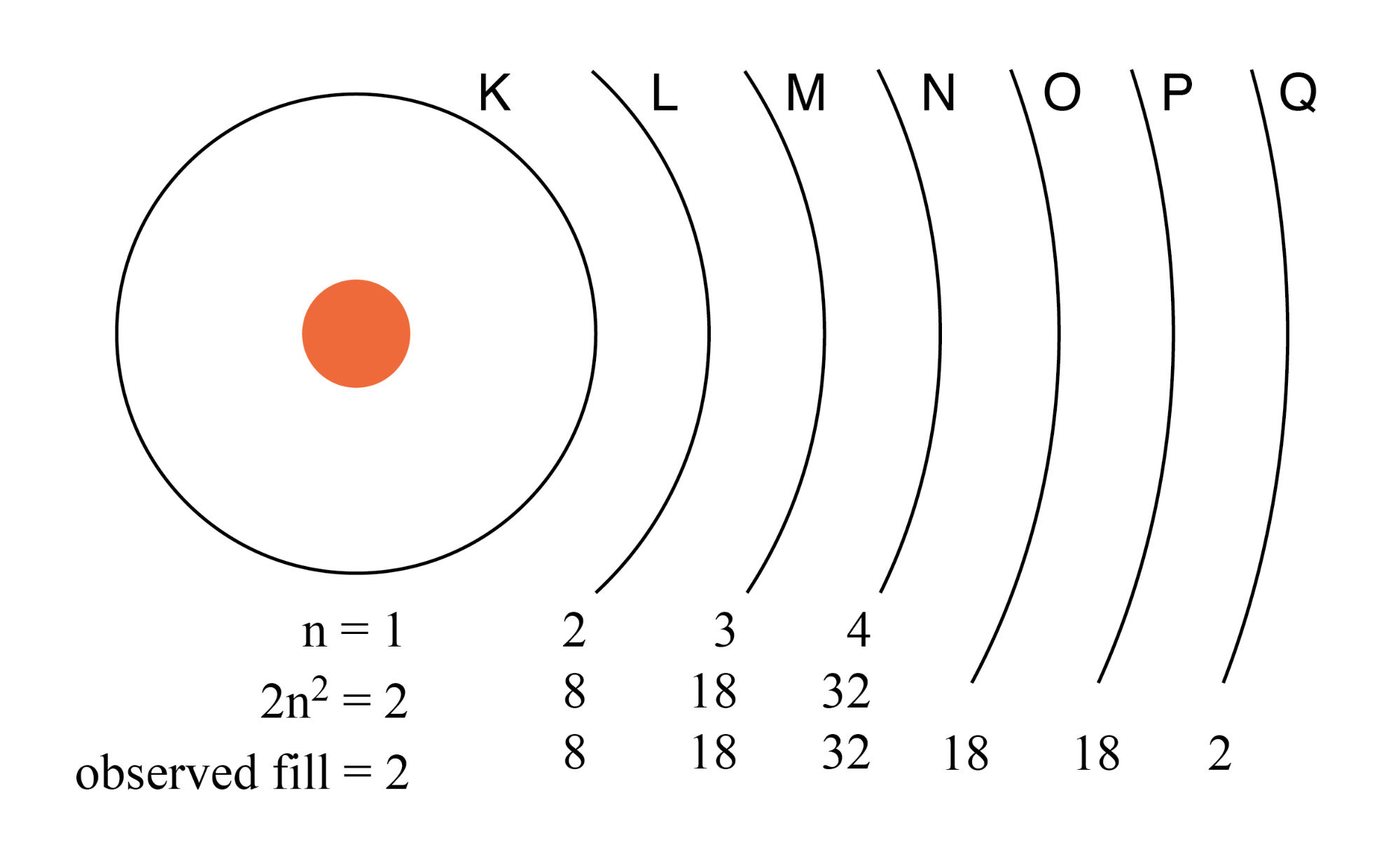
Elektronenschillen in een atoom werden vroeger aangeduid met een letter in plaats van met een nummer. De eerste schil (n=1) kreeg het label K, de tweede schil (n=2) L, de derde schil (n=3) M, de vierde schil (n=4) N, de vijfde schil (n=5) O, de zesde schil (n=6) P, en de zevende schil (n=7) Q.

2. Hoekmoment Kwantumgetal

Angular Momentum Quantum Number: Een shell, is samengesteld uit subshells. Je zou geneigd kunnen zijn om subshells te zien als eenvoudige onderverdelingen van shells, als rijstroken die een weg verdelen. De subshells zijn veel vreemder. Subshells zijn gebieden in de ruimte waar elektronen "wolken" mogen bestaan, en verschillende subshells hebben eigenlijk verschillende vormen. De eerste subschil heeft de vorm van een bol (figuur hieronder (s)), wat logisch is als het wordt gevisualiseerd als een wolk van elektronen die de atoomkern in drie dimensies omringen. De tweede subshell lijkt echter op een halter, bestaande uit twee "lobben" die op een enkel punt nabij het centrum van het atoom met elkaar zijn verbonden. (Figuur hieronder (p) ) De derde subschil lijkt typisch op een set van vier "lobben" geclusterd rond de atoomkern. Deze subshell-vormen doen denken aan grafische afbeeldingen van de signaalsterkte van de radioantenne, met bolvormige lobvormige gebieden die zich vanaf de antenne in verschillende richtingen uitstrekken. (Figuur hieronder (d) )

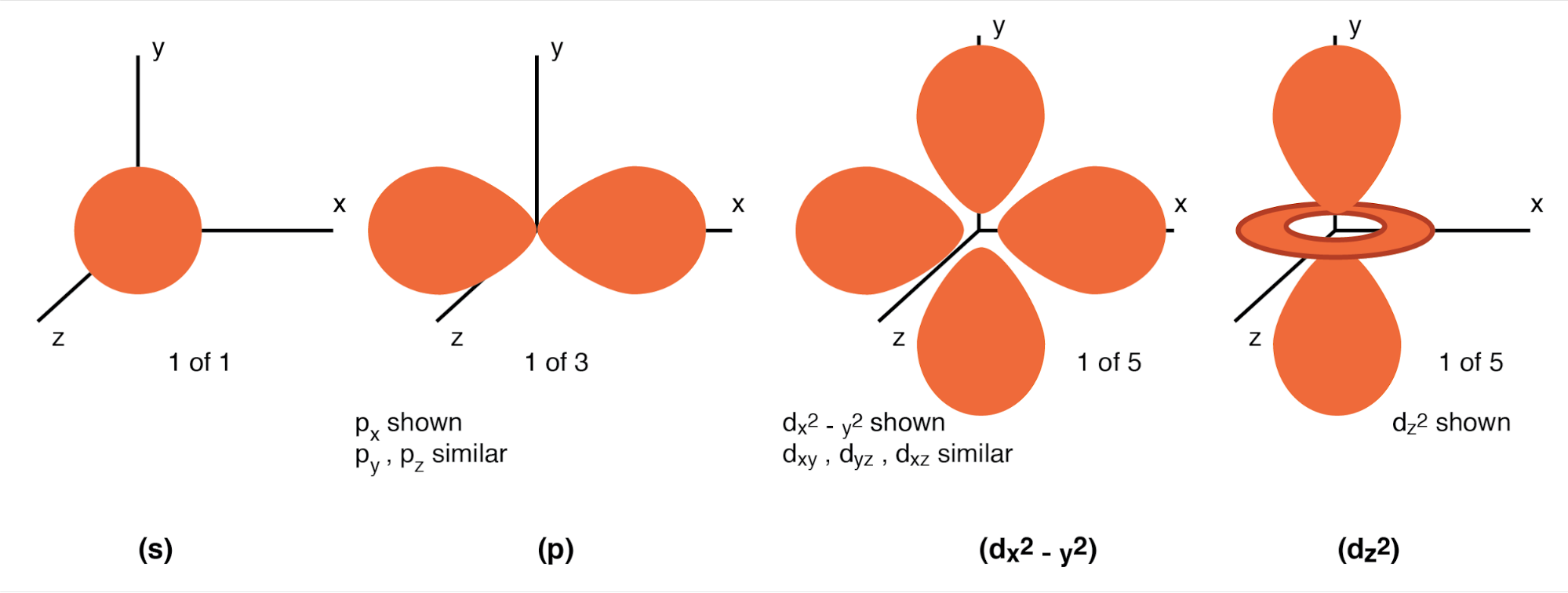
Geldige kwantumgetallen voor impulsmomenten zijn positieve gehele getallen zoals hoofdkwantumgetallen, maar bevatten ook nul. Deze kwantumgetallen voor elektronen worden gesymboliseerd door de letter l. Het aantal subshells in een shell is gelijk aan het hoofdkwantumgetal van de shell. De eerste schaal (n=1) heeft dus één subschaal, genummerd 0; de tweede schaal (n=2) heeft twee subschalen, genummerd 0 en 1; de derde schaal (n=3) heeft drie subschalen, genummerd 0, 1 en 2.

Een oudere conventie voor subshell-beschrijving gebruikte letters in plaats van cijfers. In deze notatie werd de eerste subschaal (l=0) aangeduid met s, de tweede subschaal (l=1) aangeduid met p, de derde subschaal (l=2) aangeduid met d, en de vierde subschaal (l=3) aangeduid met f. De letters komen van de woorden scherp, hoofdsom (niet te verwarren met het hoofdkwantumgetal, n), diffuus en fundamenteel. Je zult deze notatie nog steeds zien in veel periodieke tabellen, die worden gebruikt om de elektronenconfiguratie van de buitenste of valentieschillen van het atoom aan te duiden. (Figuur hieronder)

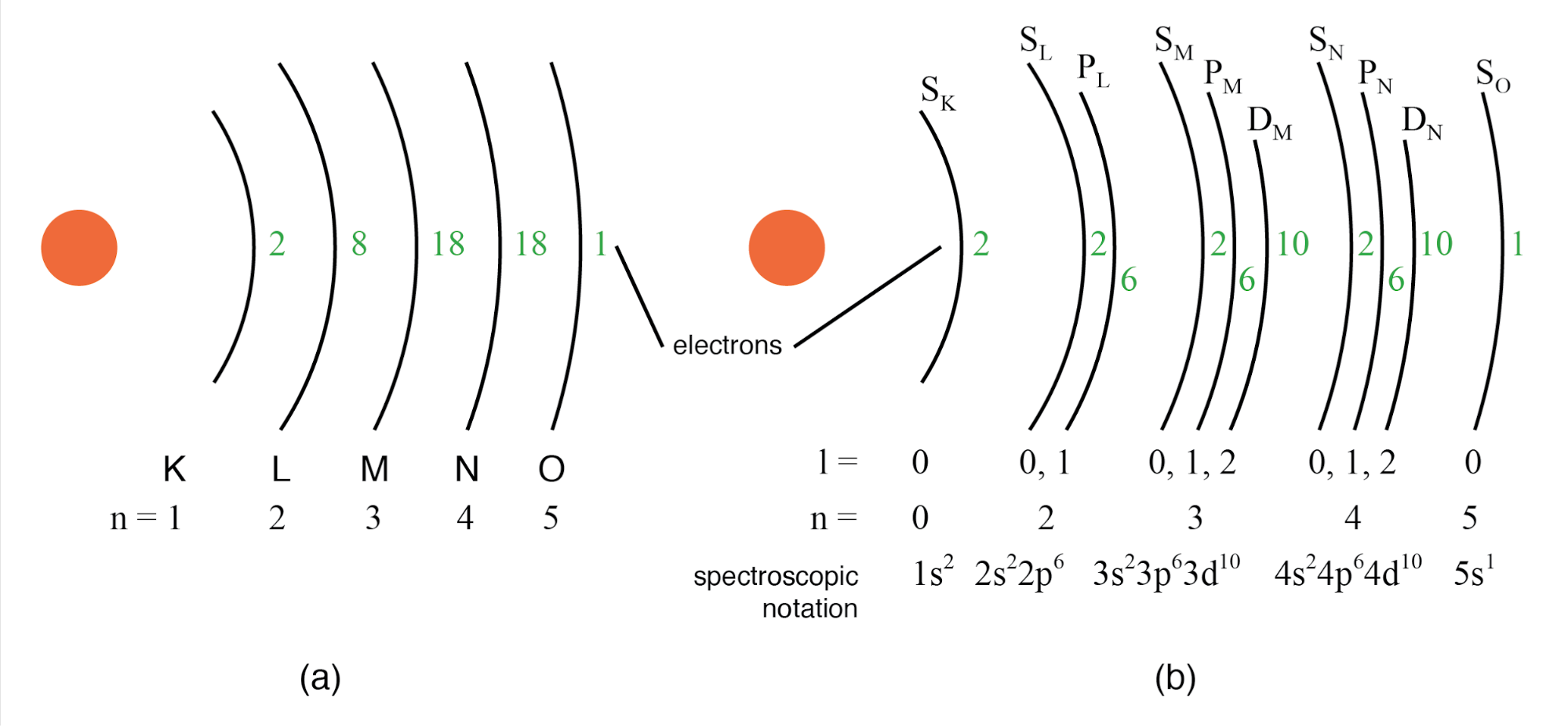
(a) Bohr-representatie van zilveratoom, (b) Subshell-representatie van Ag met verdeling van schillen in subschillen (hoekkwantumgetal l). Dit diagram zegt niets over de werkelijke positie van elektronen, maar geeft energieniveaus weer.

3. Magnetisch kwantumgetal

Magnetisch kwantumgetal: Het magnetische kwantumgetal voor een elektron classificeert in welke richting de subschaalvorm is gericht. De "lobben" voor subshells wijzen in meerdere richtingen. Deze verschillende oriëntaties worden orbitalen genoemd . Voor de eerste subshell (s; l=0), die lijkt op een bol die niet in een "richting" wijst, is er dus maar één orbitaal. Voor de tweede (p; l=1) subschaal in elke schaal, die lijkt op halters, wijzen we in drie mogelijke richtingen. Denk aan drie halters die elkaar kruisen bij de oorsprong, elk georiënteerd langs een andere as in een drieassige coördinatenruimte.

Geldige numerieke waarden voor dit kwantumgetal bestaan ​​uit gehele getallen variërend van -l tot l, en worden gesymboliseerd als m _ik in atoomfysica en l _z in de kernfysica. Om het aantal orbitalen in een bepaalde subshell te berekenen, verdubbelt u het subshell-nummer en voegt u 1, (2·l + 1) toe. De eerste subshell (l=0) in elke shell bevat bijvoorbeeld een enkele orbitaal, genummerd 0; de tweede subshell (l=1) in elke shell bevat drie orbitalen, genummerd -1, 0 en 1; de derde subshell (l=2) bevat vijf orbitalen, genummerd -2, -1, 0, 1 en 2; enzovoort.

Net als de belangrijkste kwantumgetallen, kwam het magnetische kwantumgetal rechtstreeks voort uit experimenteel bewijs:het Zeeman-effect, de verdeling van spectraallijnen door een geïoniseerd gas bloot te stellen aan een magnetisch veld, vandaar de naam "magnetisch" kwantumgetal.

4. Spin Quantum Nummer

Spin Quantum-nummer: Net als het magnetische kwantumgetal werd deze eigenschap van atomaire elektronen ontdekt door middel van experimenten. Nauwkeurige observatie van spectraallijnen onthulde dat elke lijn eigenlijk een paar zeer dicht bij elkaar liggende lijnen was, en deze zogenaamde fijne structuur werd verondersteld het gevolg te zijn van het feit dat elk elektron op een as "draaide" alsof het een planeet was. Elektronen met verschillende "spins" zouden bij opwinding licht verschillende frequenties van licht afgeven. De naam "spin" werd toegewezen aan dit kwantumnummer. Het concept van een ronddraaiend elektron is nu achterhaald en past beter bij de (onjuiste) weergave van elektronen als afzonderlijke brokken materie in plaats van als "wolken"; maar de naam blijft.

Spinkwantumgetallen worden gesymboliseerd als m _s in atoomfysica en s _z in de kernfysica. Voor elke orbitaal in elke subschil in elke schaal kunnen er twee elektronen zijn, één met een spin van +1/2 en de andere met een spin van -1/2.

Pauli-uitsluitingsprincipe

De natuurkundige Wolfgang Pauli ontwikkelde een principe dat de ordening van elektronen in een atoom volgens deze kwantumgetallen verklaart. Zijn principe, genaamd het Pauli-uitsluitingsprincipe , stelt dat geen twee elektronen in hetzelfde atoom exact dezelfde kwantumtoestanden kunnen bezetten. Dat wil zeggen, elk elektron in een atoom heeft een unieke reeks kwantumgetallen. Dit beperkt het aantal elektronen dat een bepaalde orbitaal, subschil en schil kan bezetten.

Hier wordt de elektronenrangschikking voor een waterstofatoom weergegeven:

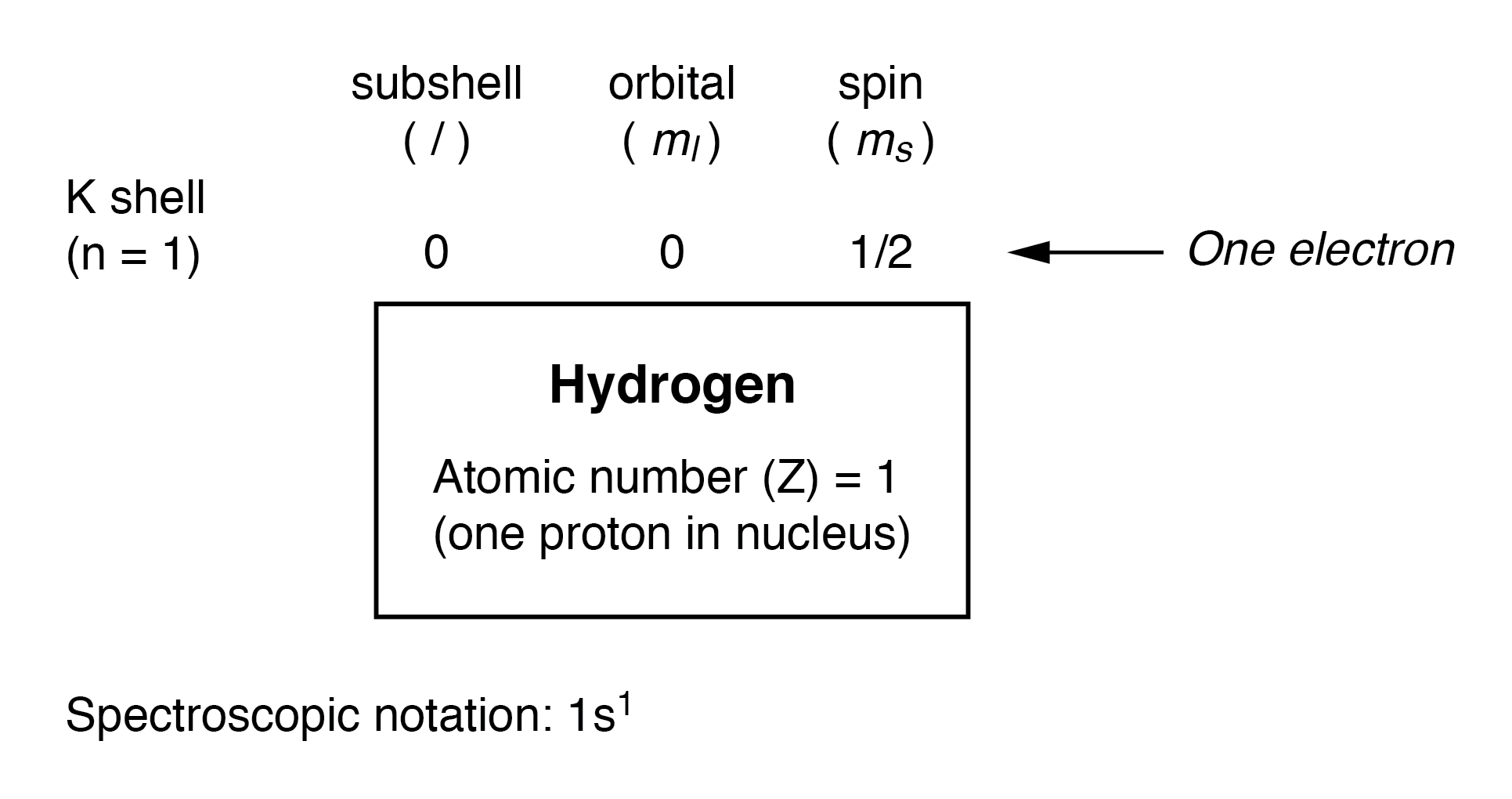
Met één proton in de kern is één elektron nodig om het atoom elektrostatisch in evenwicht te brengen (de positieve elektrische lading van het proton wordt precies in evenwicht gehouden door de negatieve elektrische lading van het elektron). Dit ene elektron bevindt zich in de onderste schil (n=1), de eerste subschil (l=0), in de enige orbitaal (ruimtelijke oriëntatie) van die subschil (m_l =0), met een spinwaarde van 1/2. Een gebruikelijke methode om deze organisatie te beschrijven is door de elektronen op te sommen volgens hun schillen en subschillen in een conventie die spectroscopische notatie wordt genoemd. . In deze notatie wordt het schaalnummer weergegeven als een geheel getal, de subschaal als een letter (s,p,d,f) en het totale aantal elektronen in de subschaal (alle orbitalen, alle spins) als een superscript. Zo wordt waterstof, met zijn enige elektron dat zich op het basisniveau bevindt, beschreven als 1s ¹ .

Als we naar het volgende atoom gaan (in volgorde van atoomnummer), hebben we het element helium:

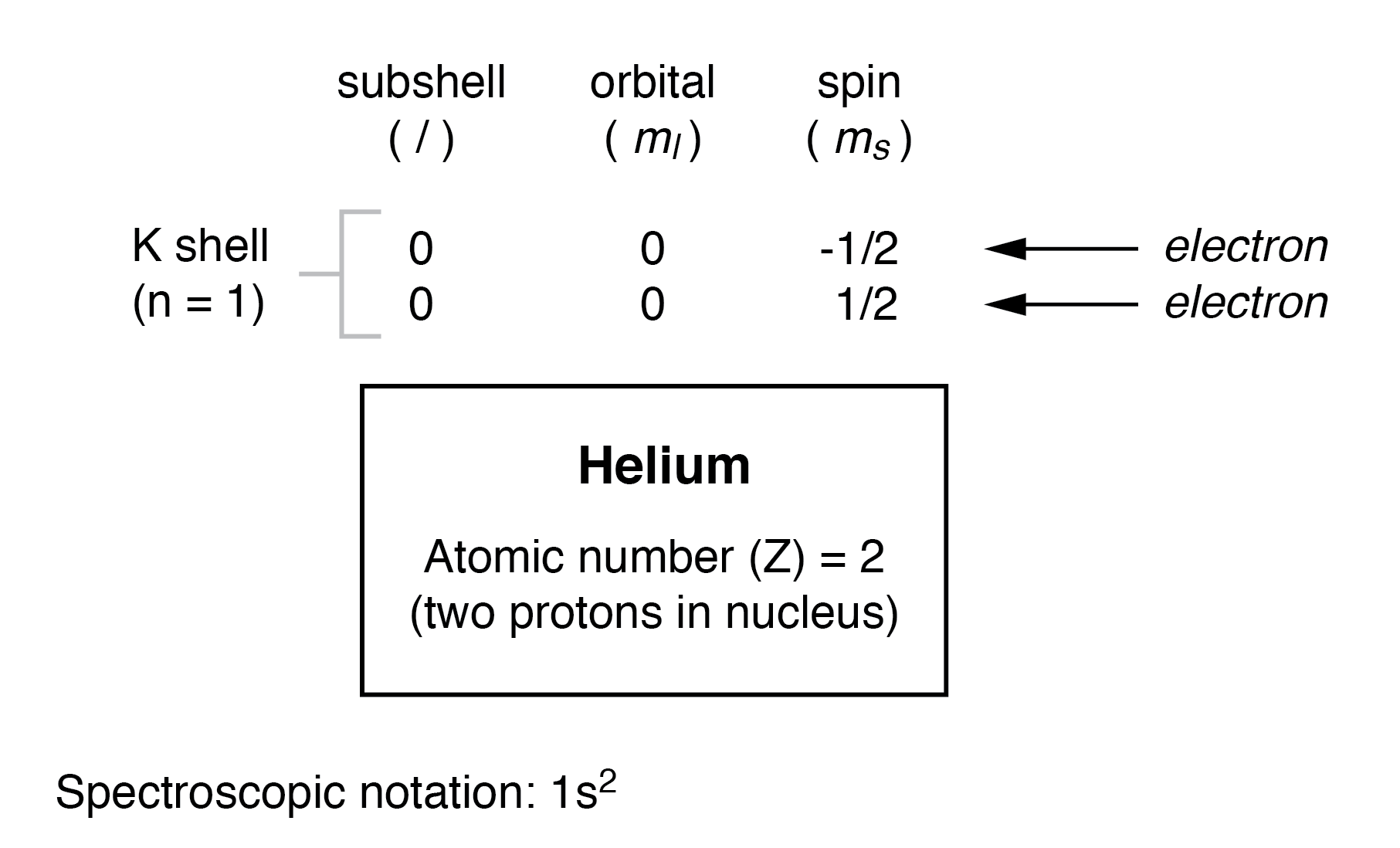
Een heliumatoom heeft twee protonen in de kern, en dit vereist twee elektronen om de dubbel-positieve elektrische lading in evenwicht te brengen. Aangezien twee elektronen - een met spin =1/2 en de andere met spin =-1/2 - in één orbitaal passen, vereist de elektronenconfiguratie van helium geen extra subschillen of schillen om het tweede elektron vast te houden.

Een atoom dat drie of meer elektronen nodig heeft, zal echter hebben extra subschillen nodig om alle elektronen vast te houden, aangezien er slechts twee elektronen in de onderste schil passen (n=1). Beschouw het volgende atoom in de reeks van toenemende atoomnummers, lithium:

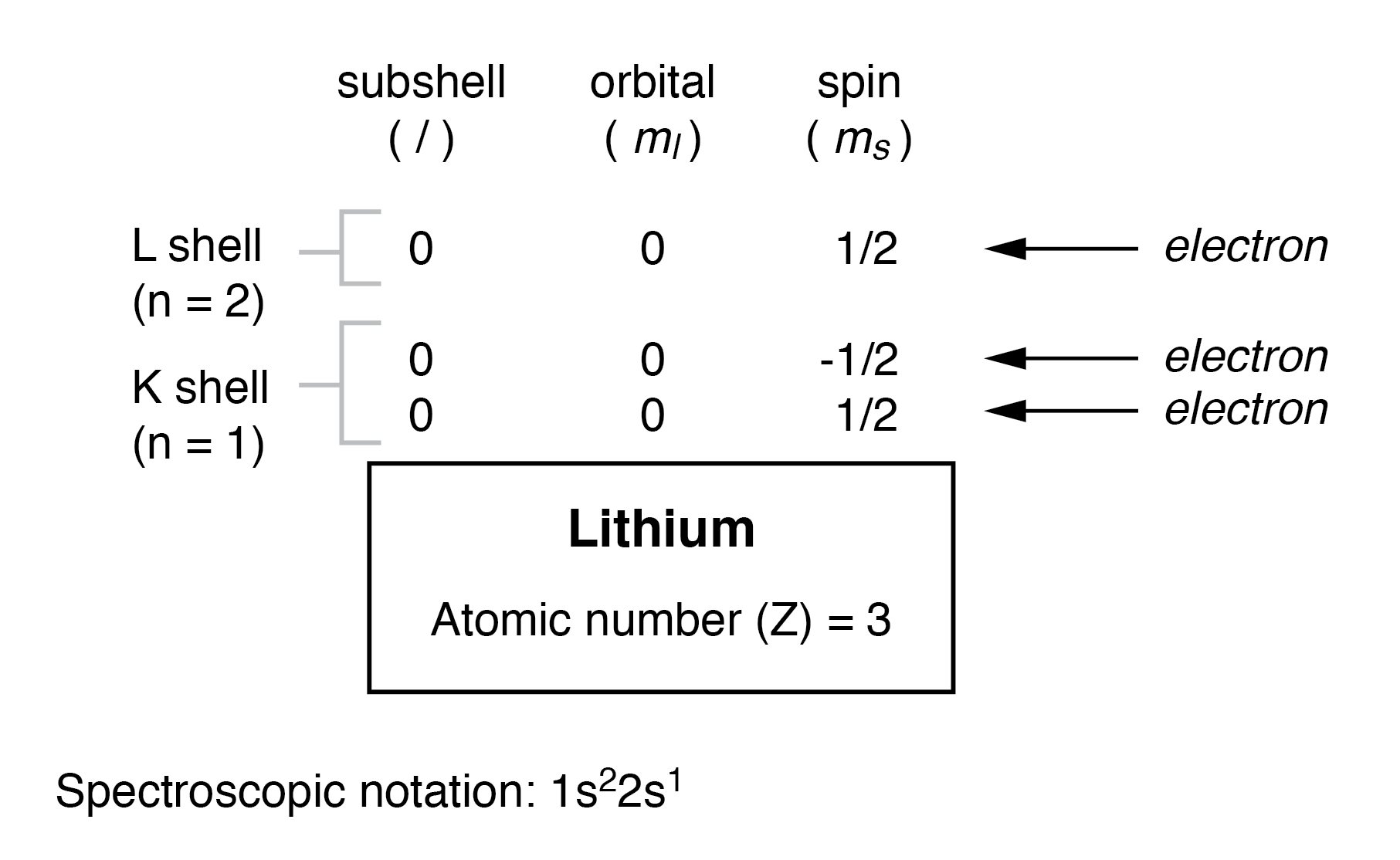
Een lithiumatoom gebruikt een fractie van de capaciteit van de L-schaal (n=2). Deze schil heeft eigenlijk een totale capaciteit van acht elektronen (maximale schilcapaciteit =2n ² elektronen). Als we de organisatie van het atoom met een volledig gevulde L-schil onderzoeken, zullen we zien hoe alle combinaties van subschillen, orbitalen en spins worden ingenomen door elektronen:

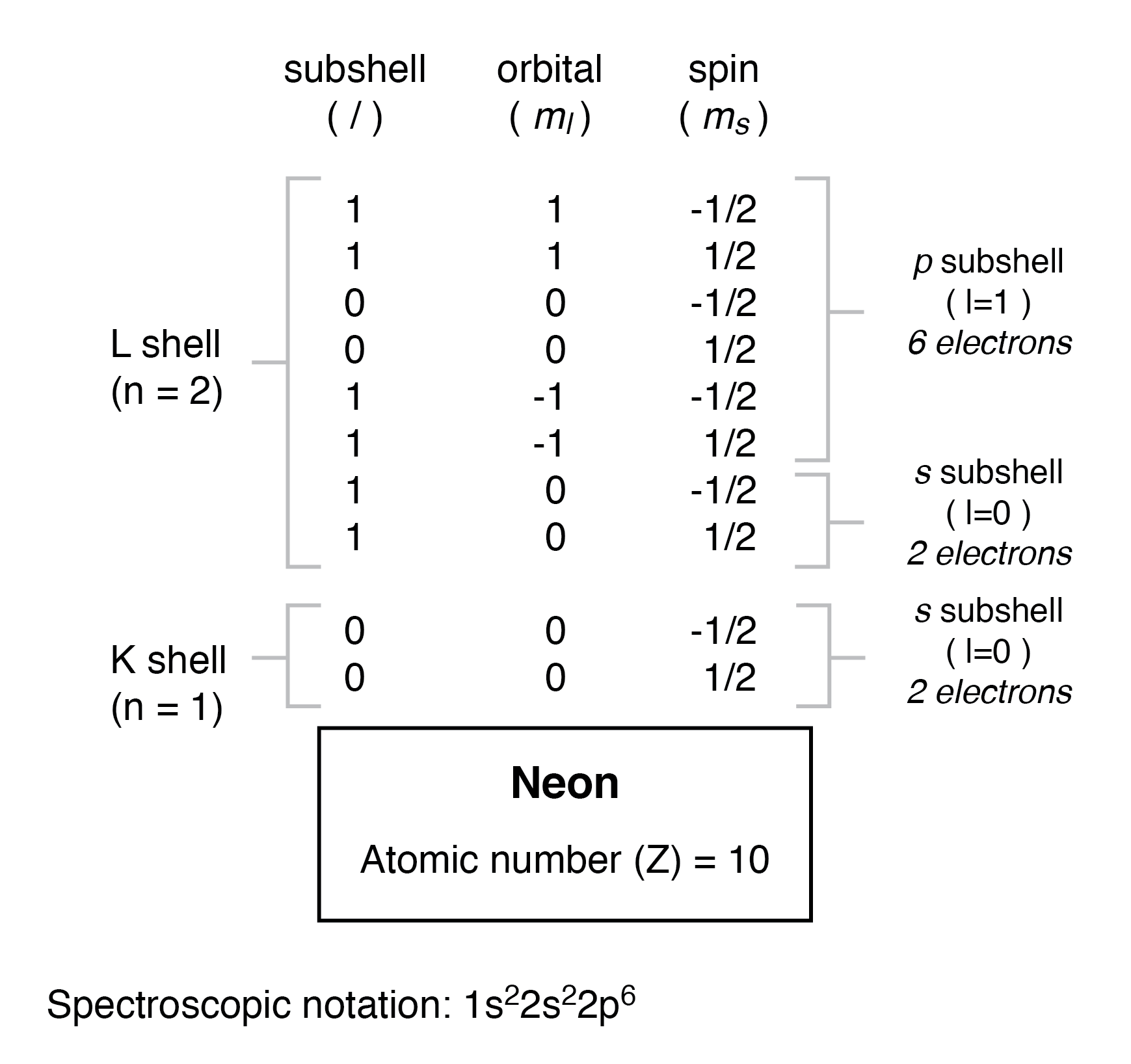
Vaak, wanneer de spectroscopische notatie voor een atoom wordt gegeven, worden alle schillen die volledig gevuld zijn weggelaten en wordt de ongevulde of de hoogste gevulde schil aangegeven. Het element neon (getoond in de vorige afbeelding), dat twee volledig gevulde schillen heeft, kan bijvoorbeeld spectroscopisch eenvoudig worden beschreven als 2p ⁶ in plaats van 1s ² 2s ² 2p ⁶ . Lithium, met zijn K-schil volledig gevuld en een eenzaam elektron in de L-schil, kan eenvoudig worden omschreven als 2s ¹ in plaats van 1s ² 2s ¹ .

Het weglaten van volledig gevulde, lager gelegen schelpen is niet alleen een notatiegemak. Het illustreert ook een basisprincipe van de chemie:dat het chemische gedrag van een element voornamelijk wordt bepaald door zijn ongevulde schillen. Zowel waterstof als lithium hebben een enkel elektron in hun buitenste schillen (1s ¹ en 2s ¹ , respectievelijk), waardoor de twee elementen enkele vergelijkbare eigenschappen hebben. Beide zijn zeer reactief en reactief op vrijwel dezelfde manier (binding aan vergelijkbare elementen in vergelijkbare modi). Het doet er weinig toe dat lithium een ​​volledig gevulde K-schaal heeft onder de bijna lege L-schaal:de ongevulde L-schaal is de schaal die het chemische gedrag bepaalt.

Elementen met een volledig gevulde buitenste schil worden geclassificeerd als edel , en onderscheiden zich door bijna volledige niet-reactiviteit met andere elementen. Deze elementen werden vroeger geclassificeerd als inert , toen men dacht dat deze volledig niet-reactief waren, maar het is nu bekend dat ze onder specifieke omstandigheden verbindingen vormen met andere elementen.

Periodiek systeem

Omdat elementen met identieke elektronenconfiguraties in hun buitenste schil (len) vergelijkbare chemische eigenschappen vertonen, heeft Dmitri Mendelejev de verschillende elementen dienovereenkomstig in een tabel gerangschikt. Zo'n tabel staat bekend als een periodiek systeem der elementen , en moderne tabellen volgen deze algemene vorm in onderstaande afbeelding.

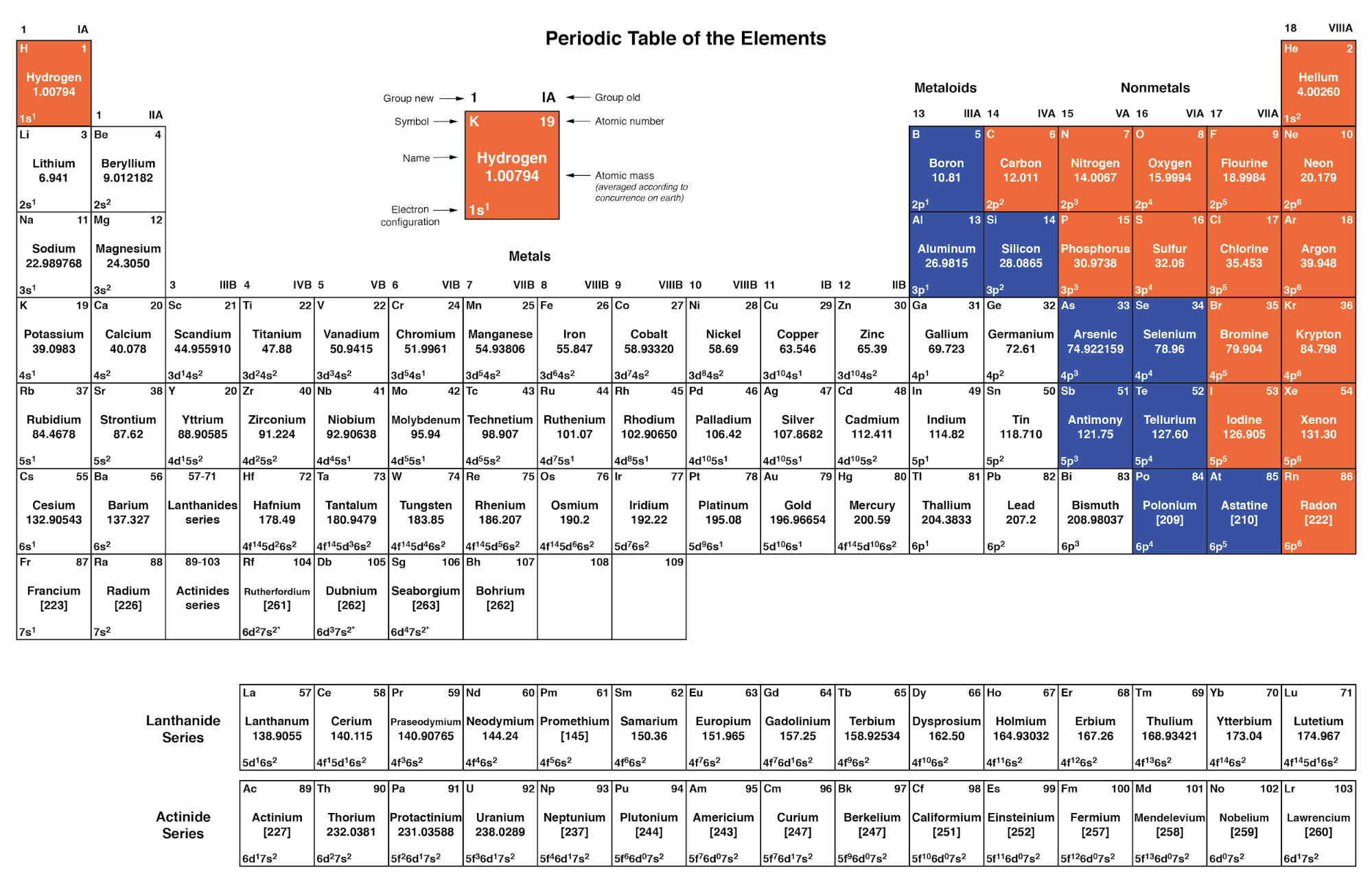
Periodiek systeem van chemische elementen

Dmitri Mendelejev, een Russische chemicus, was de eerste die een periodiek systeem van de elementen ontwikkelde. Hoewel Mendelejev zijn tafel volgens atoommassa in plaats van atoomnummer organiseerde, en een tabel produceerde die niet zo bruikbaar was als moderne periodieke tabellen, is zijn ontwikkeling een uitstekend voorbeeld van wetenschappelijk bewijs. Toen hij de patronen van periodiciteit zag (vergelijkbare chemische eigenschappen volgens de atomaire massa), veronderstelde Mendelejev dat alle elementen in dit geordende schema zouden moeten passen. Toen hij 'lege' plekken in de tafel ontdekte, volgde hij de logica van de bestaande orde en veronderstelde hij het bestaan ​​van tot nu toe onontdekte elementen. De daaropvolgende ontdekking van die elementen verleende wetenschappelijke legitimiteit aan de hypothese van Mendelejev, wat toekomstige ontdekkingen bevorderde en leidde tot de vorm van het periodiek systeem dat we vandaag gebruiken.

Dit is hoe de wetenschap zou moeten werk:hypothesen gevolgd tot hun logische conclusies, en aanvaard, gewijzigd of verworpen zoals bepaald door de overeenstemming van experimentele gegevens met die conclusies. Elke dwaas kan achteraf een hypothese formuleren om bestaande experimentele gegevens te verklaren, en velen doen dat ook. Wat onderscheidt een wetenschappelijke hypothese van post hoc speculatie is de voorspelling van toekomstige experimentele gegevens die nog niet zijn verzameld, en de mogelijkheid van weerlegging als gevolg van die gegevens. To boldly follow a hypothesis to its logical conclusion(s) and dare to predict the results of future experiments is not a dogmatic leap of faith, but rather a public test of that hypothesis, open to challenge from anyone able to produce contradictory data. In other words, scientific hypotheses are always “risky” due to the claim to predict the results of experiments not yet conducted, and are therefore susceptible to disproof if the experiments do not turn out as predicted. Thus, if a hypothesis successfully predicts the results of repeated experiments, its falsehood is disproven.

Quantum Mechanics From Hypothesis to Theory

Quantum mechanics, first as a hypothesis and later as a theory, has proven to be extremely successful in predicting experimental results, hence the high degree of scientific confidence placed in it. Many scientists have reason to believe that it is an incomplete theory, though, as its predictions hold true more at micro physical scales than at macro scopic dimensions, but nevertheless it is a tremendously useful theory in explaining and predicting the interactions of particles and atoms.

As you have already seen in this chapter, quantum physics is essential in describing and predicting many different phenomena. In the next section, we will see its significance in the electrical conductivity of solid substances, including semiconductors. Simply put, nothing in chemistry or solid-state physics makes sense within the popular theoretical framework of electrons existing as discrete chunks of matter, whirling around atomic nuclei like miniature satellites. It is when electrons are viewed as “wave functions” existing in definite, discrete states that the regular and periodic behavior of matter can be explained.

BEOORDELING:

• Electrons in atoms exist in “clouds” of distributed probability, not as discrete chunks of matter orbiting the nucleus like tiny satellites, as common illustrations of atoms show.
• Individual electrons around an atomic nucleus seek unique “states,” described by four quantum numbers :the Principal Quantum Number , known as the shell; the Angular Momentum Quantum Number , known as the subshell; the Magnetic Quantum Number , describing the orbital (subshell orientation); and the Spin Quantum Number , or simply spin . These states are quantized, meaning that no “in-between” conditions exist for an electron other than those states that fit into the quantum numbering scheme.
• The Principal Quantum Number (n ) describes the basic level or shell that an electron resides in. The larger this number, the greater radius the electron cloud has from the atom’s nucleus, and the greater that electron’s energy. Principal quantum numbers are whole numbers (positive integers).
• The Angular Momentum Quantum Number (l ) describes the shape of the electron cloud within a particular shell or level, and is often known as the “subshell.” There are as many subshells (electron cloud shapes) in any given shell as that shell’s principal quantum number. Angular momentum quantum numbers are positive integers beginning at zero and ending at one less than the principal quantum number (n-1).
• The Magnetic Quantum Number (m _l ) describes which orientation a subshell (electron cloud shape) has. Subshells may assume as many different orientations as 2-times the subshell number (l ) plus 1, (2l+1) (E.g. for l=1, ml=-1, 0, 1) and each unique orientation is called an orbital . These numbers are integers ranging from the negative value of the subshell number (l ) through 0 to the positive value of the subshell number.
• The Spin Quantum Number (m _s ) describes another property of an electron, and may be a value of +1/2 or -1/2.
• Pauli’s Exclusion Principle says that no two electrons in an atom may share the exact same set of quantum numbers. Therefore, no more than two electrons may occupy each orbital (spin=1/2 and spin=-1/2), 2l+1 orbitals in every subshell, and n subshells in every shell, and no more.
• Spectroscopic notation is a convention for denoting the electron configuration of an atom. Shells are shown as whole numbers, followed by subshell letters (s,p,d,f), with superscripted numbers totaling the number of electrons residing in each respective subshell.
• An atom’s chemical behavior is solely determined by the electrons in the unfilled shells. Low-level shells that are completely filled have little or no effect on the chemical bonding characteristics of elements.
• Elements with completely filled electron shells are almost entirely unreactive, and are called noble (formerly known as inert ).

GERELATEERDE WERKBLAD:

• Atomic Structure Worksheet
• Basic Electricity Worksheet