Cijfers en symbolen

De uitdrukking van numerieke grootheden is iets dat we als vanzelfsprekend beschouwen. Dit is zowel een goede als een slechte zaak in de studie van elektronica.

Het is goed, omdat we gewend zijn aan het gebruik en de manipulatie van getallen voor de vele berekeningen die worden gebruikt bij het analyseren van elektronische schakelingen.

Aan de andere kant is het specifieke notatiesysteem dat we vanaf de lagere school hebben geleerd niet het systeem dat intern wordt gebruikt in moderne elektronische computerapparatuur, en het leren van een ander notatiesysteem vereist een heronderzoek van diepgewortelde veronderstellingen.

Cijfers

Ten eerste moeten we onderscheid maken tussen het verschil tussen getallen en de symbolen die we gebruiken om getallen weer te geven. Een nummer is een wiskundige grootheid, die in de elektronica gewoonlijk wordt gecorreleerd aan een fysieke grootheid zoals spanning, stroom of weerstand. Er zijn veel verschillende soorten getallen. Hier zijn slechts een paar soorten, bijvoorbeeld:

HELE NUMMERS:
1, 2, 3, 4, 5, 6, 7, 8, 9 . . .

INTEGERS:
-4, -3, -2, -1, 0, 1, 2, 3, 4 . . .

IRRATIONALE NUMMERS:
π (ongeveer 3.1415927),
e (ongeveer 2.718281828),
vierkantswortel van een priemgetal

ECHTE NUMMERS:
(Alle eendimensionale numerieke waarden, negatief en positief,
inclusief nul, gehele, gehele en irrationele getallen)

COMPLEX NUMMERS:
3 - j4 , 34.5 ∠ 20 ^o

Verschillende soorten nummers vinden verschillende toepassingen in de fysieke wereld. Gehele getallen werken goed voor het tellen van discrete objecten, zoals het aantal weerstanden in een circuit. Gehele getallen zijn nodig wanneer negatieve equivalenten van gehele getallen vereist zijn.

Irrationele getallen zijn getallen die niet exact kunnen worden uitgedrukt als de verhouding van twee gehele getallen, en de verhouding van de omtrek van een perfecte cirkel tot zijn diameter (π) is hier een goed fysiek voorbeeld van. De niet-gehele hoeveelheden spanning, stroom en weerstand waarmee we in gelijkstroomcircuits te maken hebben, kunnen worden uitgedrukt als reële getallen, in fractionele of decimale vorm.

Voor AC-circuitanalyse slagen reële getallen er echter niet in om de dubbele essentie van grootte en fasehoek vast te leggen, en daarom wenden we ons tot het gebruik van complexe getallen in rechthoekige of polaire vorm.

Symbolen

Als we getallen willen gebruiken om processen in de fysieke wereld te begrijpen, wetenschappelijke voorspellingen te doen of onze chequeboekjes in evenwicht te brengen, moeten we een manier hebben om ze symbolisch aan te duiden.

Met andere woorden, we kunnen misschien weten hoeveel geld we op onze betaalrekening hebben, maar om het bij te houden, moeten we een systeem hebben om die hoeveelheid op papier te symboliseren, of in een andere vorm voor het bijhouden en volgen.

Analoog en digitaal

Er zijn twee basismanieren waarop we dit kunnen doen:analoog en digitaal. Bij analoge weergave wordt de hoeveelheid gesymboliseerd op een manier die oneindig deelbaar is. Bij digitale weergave wordt de hoeveelheid gesymboliseerd op een discrete manier verpakt.

Analoge weergave

U bent waarschijnlijk al bekend met een analoge weergave van geld en besefte niet wat het was. Heb je ooit een inzamelingsposter gezien met een afbeelding van een thermometer erop, waarbij de hoogte van de rode kolom het bedrag aangaf dat voor het goede doel was ingezameld? Hoe meer geld er wordt ingezameld, hoe groter de kolom rode inkt op de poster.

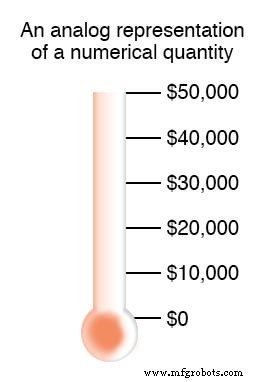
Dit is een voorbeeld van een analoge weergave van een getal. Er is geen echte limiet aan hoe fijn verdeeld de hoogte van die kolom kan worden gemaakt om de hoeveelheid geld op de rekening te symboliseren. Het veranderen van de hoogte van die kolom is iets dat gedaan kan worden zonder de essentiële aard van wat het is te veranderen.

Lengte is een fysieke hoeveelheid die zo klein kan worden verdeeld als je wilt, zonder praktische limiet. De rekenliniaal is een mechanisch apparaat dat dezelfde fysieke hoeveelheid (lengte) gebruikt om getallen weer te geven en om rekenkundige bewerkingen met twee of meer getallen tegelijk uit te voeren. Het is ook een analoog apparaat.

Digitale weergave

Aan de andere kant, een digitale weergave van datzelfde geldbedrag, geschreven met standaardsymbolen (soms cijfers genoemd), ziet er als volgt uit:

$ 35.955,38

In tegenstelling tot de "thermometer"-poster met zijn rode kolom, kunnen die symbolische tekens hierboven niet fijn worden verdeeld:die specifieke combinatie van cijfers staat voor één hoeveelheid en slechts voor één hoeveelheid.

Als er meer geld aan de rekening wordt toegevoegd (+ $ 40,12), moeten verschillende symbolen worden gebruikt om het nieuwe saldo ($ 35.995,50) weer te geven, of in ieder geval dezelfde symbolen in verschillende patronen. Dit is een voorbeeld van digitale weergave.

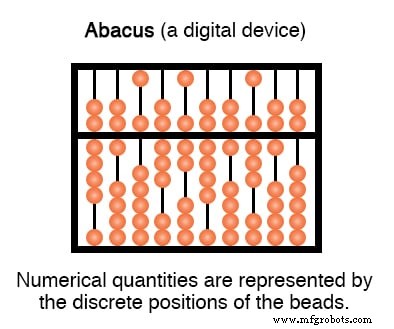
De tegenhanger van de rekenliniaal (analoog) is ook een digitaal apparaat:het telraam, met kralen die op staafjes heen en weer worden bewogen om numerieke grootheden te symboliseren:

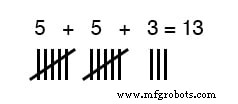
Contrast tussen analoge en digitale weergave

Laten we deze twee methoden van numerieke representatie tegenover elkaar stellen:

ANALOGE DIGITAAL
---------------------------------------------- --------------------
Intuïtief begrepen ----------- Vereist training om te interpreteren
Oneindig deelbaar --- ----------- Discreet
Gevoel voor precisiefouten ------ Absolute precisie

Interpretatie van numerieke symbolen is iets dat we als vanzelfsprekend beschouwen omdat het ons al vele jaren is geleerd. Als u echter zou proberen een hoeveelheid van iets door te geven aan een persoon die geen kennis heeft van decimale cijfers, zou die persoon nog steeds de eenvoudige thermometergrafiek kunnen begrijpen!

De oneindig deelbare vs. discrete en nauwkeurige vergelijkingen zijn in feite de keerzijde van dezelfde medaille. Het feit dat digitale weergave is samengesteld uit afzonderlijke, discrete symbolen (decimale cijfers en telraamkralen), betekent noodzakelijkerwijs dat het in staat zal zijn om hoeveelheden in precieze stappen te symboliseren.

Aan de andere kant is een analoge weergave (zoals de lengte van een rekenliniaal) niet samengesteld uit afzonderlijke stappen, maar eerder uit een continu bewegingsbereik. De mogelijkheid voor een rekenliniaal om een ​​numerieke hoeveelheid te karakteriseren tot oneindige resolutie is een compromis voor onnauwkeurigheid.

Als er tegen een rekenliniaal wordt gestoten, wordt een fout geïntroduceerd in de weergave van het nummer dat erin is "ingevoerd". Er moet echter veel harder tegen een telraam worden gestoten voordat de kralen volledig van hun plaats zijn verwijderd (voldoende om een ​​ander getal weer te geven).

Begrijp dit verschil in precisie niet verkeerd door te denken dat digitale weergave noodzakelijkerwijs nauwkeuriger is dan analoog. Het feit dat een klok digitaal is, betekent niet dat hij de tijd altijd nauwkeuriger zal lezen dan een analoge klok, het betekent alleen dat de interpretatie van het display is minder dubbelzinnig.

Deelbaarheid van analoge versus digitale representatie kan verder worden verlicht door te praten over de representatie van irrationele getallen. Getallen zoals π worden irrationeel genoemd, omdat ze niet exact kunnen worden uitgedrukt als de breuk van gehele getallen of gehele getallen.

Hoewel je in het verleden misschien hebt geleerd dat de breuk 22/7 kan worden gebruikt voor π in berekeningen, is dit slechts een benadering. Het werkelijke aantal "pi" kan niet exact worden uitgedrukt door een eindig of beperkt aantal decimalen. De cijfers van π gaan voor altijd door:

3.1415926535897932384 . . . . .

Het is, althans theoretisch, mogelijk om een ​​rekenliniaal (of zelfs een thermometerkolom) zo in te stellen dat het getal π perfect wordt weergegeven, omdat analoge symbolen geen minimumlimiet hebben in de mate waarin ze kunnen worden verhoogd of verlaagd.

Als mijn rekenliniaal een cijfer van 3.141593 toont in plaats van 3.141592654, kan ik de dia iets meer (of minder) stoten om het nog dichterbij te krijgen. Met digitale weergave, zoals met een telraam, zou ik echter extra staafjes (plaatshouders of cijfers) nodig hebben om π met een grotere nauwkeurigheid weer te geven.

Een telraam met 10 staven kan simpelweg niet meer dan 10 cijfers van het getal π vertegenwoordigen, ongeacht hoe ik de kralen plaats. Om π perfect weer te geven, zou een telraam een ​​oneindig aantal kralen en staafjes moeten hebben! De afweging is natuurlijk de praktische beperking tot het aanpassen en lezen van analoge symbolen.

In de praktijk kan men de schaal van een rekenliniaal niet aflezen tot op het tiende cijfer van de precisie, omdat de markeringen op de schaal te grof zijn en het menselijk zicht te beperkt is. Een telraam daarentegen kan worden ingesteld en gelezen zonder enige interpretatiefout.

Bovendien vereisen analoge symbolen een soort standaard waarmee ze kunnen worden vergeleken voor nauwkeurige interpretatie. Rekenlinialen hebben markeringen gedrukt langs de lengte van de dia's om de lengte om te zetten in standaard hoeveelheden.

Zelfs de thermometerkaart heeft cijfers die langs de hoogte zijn geschreven om aan te geven hoeveel geld (in dollars) de rode kolom vertegenwoordigt voor een bepaalde hoogte. Stel je voor dat we allemaal zouden proberen om eenvoudige getallen aan elkaar door te geven door onze handen op verschillende afstanden uit elkaar te houden.

Het nummer 1 kan worden aangeduid door onze handen 1 inch uit elkaar te houden, het nummer 2 met 2 inch, enzovoort. Als iemand zijn handen 17 inch uit elkaar zou houden om het getal 17 weer te geven, zou iedereen om hen heen dan in staat zijn om die afstand onmiddellijk en nauwkeurig als 17 te interpreteren? Waarschijnlijk niet.

Sommigen zouden kort raden (15 of 16) en sommigen zouden lang raden (18 of 19). Natuurlijk vinden vissers die opscheppen over hun vangsten geen bezwaar tegen overschattingen in kwantiteit!

Misschien is dit de reden waarom mensen over het algemeen hebben gekozen voor digitale symbolen voor het weergeven van getallen, met name gehele getallen en gehele getallen, die in het dagelijks leven het meest worden toegepast.

Met de vingers van onze handen hebben we een handig middel om gehele getallen van 0 tot 10 te symboliseren. We kunnen vrij gemakkelijk hekjes maken op papier, hout of steen om dezelfde hoeveelheden weer te geven:

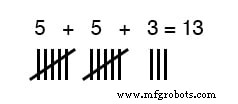
Voor grote getallen is het "hashteken"-nummeringssysteem echter te inefficiënt.