Wat is de Fourier-transformatie?

Dit artikel geeft je essentiële informatie over een wiskundige techniek die een absoluut fundamentele rol speelt in systeemontwerp en signaalverwerking.

De Fourier-transformatie, genoemd naar de Franse wiskundige Joseph Fourier, is een wiskundige procedure waarmee we de frequentie-inhoud kunnen bepalen. van een functie. Voor elektrotechnici wordt de Fourier-transformatie meestal toegepast op tijdfuncties die we signalen noemen .

Sinusvormige ontbinding

Een plot van spanning of stroom versus tijd, zoals we zouden zien op een oscilloscoopscherm, is een intuïtieve weergave van signaalgedrag. Het is echter niet de enige bruikbare weergave.

In veel gevallen, bijvoorbeeld bij het ontwerp van RF-systemen, zijn we vooral geïnteresseerd in het periodieke gedrag van signalen. Meer specifiek zijn we geïnteresseerd in het begrijpen van een signaal met betrekking tot sinusoïdaal periodiciteit, omdat sinusoïden de unieke wiskundige uitdrukking zijn van "pure" frequentie.

De Fourier-transformatie onthult de elementaire periodiciteit van een signaal door ontbinden het signaal in zijn samenstellende sinusoïdale frequenties en het identificeren van de grootten en fasen van deze samenstellende frequenties.

Het woord "ontbindend" is hier cruciaal. De Fourier-transformatie leert ons een tijddomeinsignaal te beschouwen als een golfvorm die uit is samengesteld. onderliggende sinusoïdale golfvormen met verschillende grootten en fasen.

Een blokgolf kan bijvoorbeeld worden ontleed in een oneindige reeks sinusoïden met amplitudes die gestaag afnemen en frequenties die gestaag toenemen. De exacte reeks, voor een AC-gekoppelde blokgolf met periode T en amplitude A, kan als volgt worden geschreven:

\[f_{square}(t)=\frac{4A}{\pi}\sum_{k\in{\{1,3,5,...\ }}}\frac{1}{k}\sin\left(\frac{2\pi kt}{T}\right)\]

We kunnen dit omzetten in de volgende vorm, die iets intuïtiever is:

\[f_{square}(t)=\frac{4A}{\pi}\left(\sin(2\pi ft)+\frac{1}{3 }\sin(6\pi ft)+\frac{1}{5}\sin(10\pi ft)+\ ...\right)\]

waarbij f de frequentie is, in hertz, van de blokgolf.

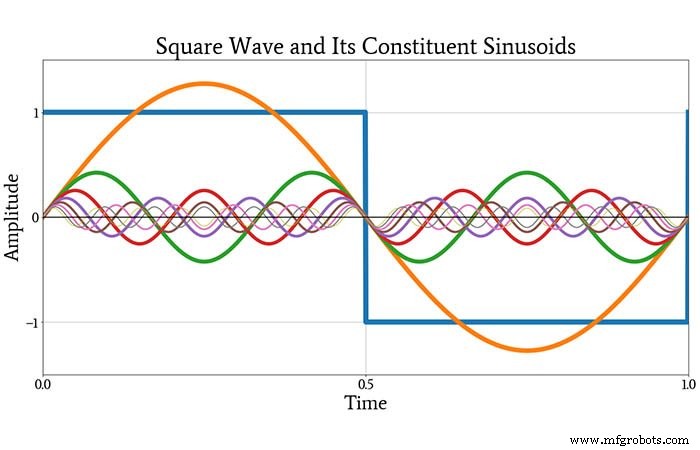
De volgende grafiek toont de originele blokgolf, in blauw, en de eerste acht sinusoïden in de oneindige reeks.

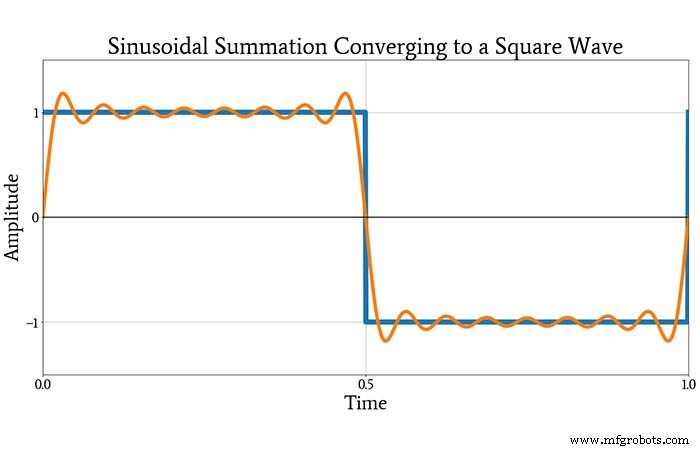
Na het bekijken van deze plot, ben je misschien nog steeds een beetje sceptisch dat deze sinusoïden kunnen worden gecombineerd tot een blokgolf. Het volgende plot zal je echter overtuigen. Het toont de originele blokgolf en de golfvorm geproduceerd door toevoegen alle samenstellende sinusoïden die hierboven zijn weergegeven.

Functies van tijd en frequentie

Wanneer we een Fourier-transformatie berekenen, beginnen we met een functie van de tijd, f(t), en via wiskundige ontleding produceren we een functie van de frequentie, F(ω). (We gebruiken meestal hoekfrequentie in theoretische discussies over de Fourier-transformatie.)

Het evalueren van F(ω) bij een bepaalde hoekfrequentie, zeg 100 rad/s, geeft ons de grootte en fase van de sinusoïdale component van f(t) met een frequentie van 100 rad/s. Als f(t) geen sinusvormige component heeft bij 100 rad/s, is de magnitude nul.

Je vraagt ​​je misschien af ​​hoe één functie, F(ω), zowel de grootte als de fase kan rapporteren. De Fourier-transformatie produceert een complex-waarded functie, wat betekent dat de transformatie zelf noch de grootte van de frequentiecomponenten in f(t) is, noch de fase van deze componenten. Zoals bij elk complex getal, moeten we aanvullende berekeningen uitvoeren om de grootte of de fase te extraheren.

Het concept van een transformatie met complexe waarden is iets intuïtiever als we werken met een discrete Fourier-transformatie, in plaats van een 'standaard'-transformatie waarin we beginnen met een symbolische functie van tijd en eindigen met een symbolische functie van frequentie.

De discrete Fourier-transformatie werkt op een reeks numerieke waarden en produceert een reeks Fourier coëfficiënten . Deze coëfficiënten zijn typische complexe getallen (d.w.z. ze hebben de vorm a + jb), en we gebruiken meestal de grootte van deze complexe getallen, berekend als √(a ² +b ² ), bij het analyseren van de frequentie-inhoud van een signaal.

De Fourier-transformatie plotten

Percelen met frequentie-inhoud komen zeer vaak voor in datasheets, testrapporten, studieboeken, enzovoort. We verwijzen vaak naar een plot van magnitude versus frequentie als een spectrum - bijvoorbeeld:"laten we eens kijken naar het spectrum van het signaal" betekent "laten we eens kijken naar een soort visuele representatie van de magnitude-informatie in de Fourier-transformatie .”

De volgende grafiek toont het spectrum van een AC-gekoppelde blokgolf met een amplitude van 1 en een frequentie van 1 Hz.

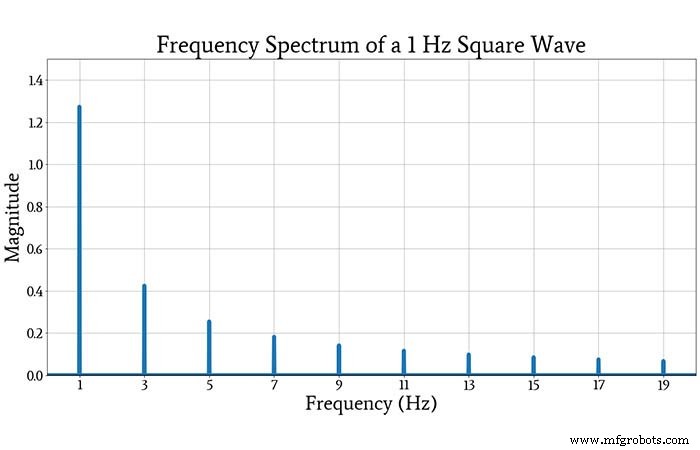
Als je de uitgezette amplitudes van de frequentie-"pieken" vergelijkt met de amplitudes van de corresponderende sinusoïdale componenten in de oneindige reeks die hierboven is besproken, zul je zien dat ze consistent zijn.

De Fourier-transformatie berekenen

We zijn bijna aan het einde van dit artikel en ik heb je nog steeds niet verteld hoe we de Fourier-transformatie van een wiskundig gedefinieerd signaal genereren.

Om eerlijk te zijn, zie ik geen noodzaak om wiskundige details grondig te onderzoeken in een inleidend artikel:frequentie-domeinanalyse wordt tegenwoordig gedomineerd door gebruiksvriendelijke, op software gebaseerde technieken, en ingenieurs besteden niet veel tijd aan het omzetten van symbolische tijd- domeinuitdrukkingen in symbolische frequentiedomeinuitdrukkingen.

Niettemin, met zoiets belangrijks als de Fourier-transformatie, is het goed om je op zijn minst bewust te zijn van de onderliggende wiskunde. Dus, zonder verder oponthoud, dit is hoe we f(t) omzetten in F(ω):

\[F(\omega ) =\int\limits_{ - \infty }^{ + \infty } {f(t){e^{ - j\omega t} }dt}\]

Conclusie

Ik hoop dat dit artikel een duidelijke, intuïtieve uitleg heeft gegeven van wat de Fourier-transformatie is en hoe deze ons extra inzicht geeft in de aard van een signaal.

De Fourier-transformatie is slechts het begin van een uitgebreide reeks gerelateerde onderwerpen; als je meer wilt weten, bekijk dan de onderstaande artikelen.

Verder lezen

• Een inleiding tot de discrete Fourier-transformatie
• Een inleiding tot de snelle Fourier-transformatie
• Frequentie-domeinanalyse uitvoeren met Scilab
• Leren leven in het frequentiedomein
• Lineaire filtering op basis van de discrete Fourier-transformatie